La Conjetura de Riemann
Paulo Manrique
El Dr. Paulo César Manrique Mirón es ingeniero matemático de la Escuela Superior de Física y Matemática del IPN, con doctorado en Probabilidad y Estadística del Centro en Investigaciones Matemáticas. Actualmente es investigador catedrático en el programa de Cátedras del CONACyT. Se dedica al estudio de los problemas donde el azar está presente, además de colaborar con personas de otras áreas, como la medicina, para modelar el azar en sus respectivas áreas.
El jueves de 20 de septiembre de 2018, mientras leía los mensajes recibidos en mi correo electrónico, hubo uno que llamó mi atención. El título del mensaje, “Conjetura de Riemann”. Su contenido mencionaba que existía un “chisme” en las redes sociales de que Sir Michael Francis Atiyah presentaría el lunes siguiente una prueba para esa conjetura. Después de leer su contenido, me dirigí a la Internet para indagar más al respecto. Efectivamente encontré mucha información sobre lo que sucedería al lunes siguiente en un evento llamado Foro de Heidelberg.
La razón de que el mensaje y el anunció de la conferencia en el Foro de Heidelberg llamara inmediatamente mi atención, era que ya hace algunos años se habían resuelto la Conjetura de Poincaré, por Grigori Perelman, y la Conjetura de Fermat, por Andrew Wiles. Cabe decir estas ya no son conjeturas, ahora son teoremas, es decir, hechos matemáticos que han sido demostrados. Hasta el momento no se han encontrado errores en los argumentos empleados para verificarlas, pero en cualquier momento alguien puede decir “miren aquí un error”, lo cual sucede con mucha frecuencia. Por lo que pensar que la posibilidad que Atiyah, famoso y renombrado matemático británico, realmente hubiera llegado a una solución a otro de los Problemas del Milenio era totalmente plausible. Como mencionaré más adelante, el interés de resolver algunos de estos problemas son interés puramente matemático, es decir, son problemas surgidos en las matemáticas y cuyas soluciones son útiles para las matemáticas. Sin embargo, se puede encontrar una utilidad práctica a estos teoremas, como por ejemplo en el estudio del cáncer[1].
 La primera vez que escuché sobre el problema
La primera vez que escuché sobre el problema
Como muchos estudiantes de matemáticas durante su formación, fui conociendo sobre los problemas abiertos que han captado la atención de muchos matemáticos durante mucho tiempo, como el Problema de los Cuatro Colores, la Conjetura de Fermat, la Conjetura de Poincaré, la Conjetura de Riemann, la Conjetura de Goldbach, etc. (Y las demás conjeturas que faltan ir descubriendo).
En mi clase de Variable Compleja fue la primera vez que escuché sobre la Conjetura de Riemann, donde se me presentó de manera formal a la Función Zeta de Riemann, la cual es la expresión matemática con la que se establece la mencionada conjetura. La Variable Compleja es una extensa área de las matemáticas en las que se estudian las relaciones que existen y que se puedan establecer entre los números complejos. El profesor nos explicó sobre la convergencia de series infinitas de números complejos.
¿Qué tipos de números existen?
Antes de hablar un poco más de lo que son los números complejos y las series infinitas, necesario poder entender un poco mejor qué es la Función Zeta de Riemann, hay que hablar sobre los diferentes tipos de números que existen. Aunque para muchos pueda sonar algo raro o, incluso, sin importancia, hay que saber qué hasta el día de hoy se han establecido diferentes tipos de números. Los primeros números que se aprendemos son los “números naturales”. Se llaman así porque con ellos se hace algo que naturalmente hacemos los humanos, contar. Para representarlos se usan los símbolos 1, 2, 3, etc. Después, tenemos a los números fraccionarios, los cuales se emplean cuando se quiere hacer referencia a una parte de un todo y que suelen representarse con una diagonal entre dos números naturales, 1/2, 1/3, etc. Por ejemplo, es común escuchar expresiones como “quiero medio kilo de limones”, con lo que se expresa la idea de que, en lugar de pedir un kilogramo de limones, sólo se solicita la mitad de dicha unidad de medida. Estos dos tipos de números son los que regularmente todas las personas usamos en nuestra vida cotidiana.
Cuando se llega a cierto nivel escolar, es cuando se sabe que existen los números positivos y los números negativos. En términos sencillos, son números fraccionarios o naturales a los cuales que se les agrega un signo más + o un signo menos -, para indicarlos respectivamente. Estos números con signo se usan para explicar la manera en que se resuelven ecuaciones del tipo x+1=0. Y aunque no sean tan usados por las personas, son muy útiles al momento de para indicar ideas de subida y bajada de precios, calificaciones o temperaturas.
Otro tipo de números son los números irracionales. Posiblemente este tipo de número nos resulte completamente ajeno, pero muchos conocemos el número pi (π), el cual es un ejemplo usual de los números irracionales. Hay que recordar que el número pi sirve, entre muchas otras cosas, para calcular el área de un círculo. El número pi (Figura 1) es tan famoso que incluso existe un día en su honor, llamado el Día Pi [2] (celebrado cada 14 de marzo).
Números complejos sin “complejos”
Ahora, hablemos un poco de los números complejos. En términos concretos, un número complejo es aquel que tiene la forma z=a+ib, donde a y b son cualesquiera de los tipos de números que ya se han mencionado. En este caso, i es un número especial, que tiene la propiedad de que si lo multiplicamos por sí mismo (i por i), el resultado será -1, que es un número negativo. Al valor de a se le conoce como la parte real de z y al número b la parte imaginaria de z. Aunque parezca algo complicado, la aplicación de los números complejos podemos encontrarla en cosas tan importantes como el diseño del ala de un avión, donde es vital tener una sección cuya forma permita que el aire fluya sin turbulencias. Esto solamente se logra si se utilizan las formas aerodinámicas de Jouwkoski[3] las cuales involucran números complejos con la forma mencionada anteriormente.
Los números complejos, a pesar de su aparente complejidad, son una gran herramienta que ayuda a entender de una mejor manera varios fenómenos físicos, como las señales sonoras y además ellos permiten crear algoritmos que mejoran la resolución de las imágenes (e incluso vídeo) en una computadora.
Al infinito y más allá…
Regresando a la cuestión de la Conjetura de Riemann y a mi clase de Variable Compleja, preguntarse si la suma de una cantidad infinita de números complejos existe, es también una cuestión común. Por ejemplo, si se considera la suma 1 + 1 + 1 + …, se puede deducir, sin mucho problema, que el valor de ella va creciendo sin parar. Pero, ¿qué sucede con si tiene la suma 1+1/2+1/4+1/8+1/16+1/32+…? Se puede notar que cada vez se van agregando cantidades más pequeñas, por lo que podría pensarse que la suma debería acercarse a un número fijo, y (aunque no explicaré ésto detalladamente), se puede hacer ver que la última suma es igual a 2, 2=1+1/2+1/4+1/8+1/16+1/32+… (curioso, ¿no?).
La suma entre números complejos se hace sumando respectivamente las partes reales y las partes imaginarias, (1-3i) + (1+2i) = 2 – i. Llegado a este punto alguien puede preguntar qué utilidad puede tener sumar una cantidad infinita de números, la respuesta concreta y sencilla, sumar es la idea más básica y útil de las matemáticas. Pero antes de presentar a la Función Zeta de Riemann, quiero mencionar que entre las operaciones que se realizan entre los números, existe la “potenciación” o potencia, que en su forma más básica significa multiplicar un número por sí mismo, una cierta cantidad de veces. Por ejemplo, 32=3*3=9 y si recordamos algo de nuestras clases de matemáticas, al 3 se le llama la base de la potencia, al 2 el exponente de la potencia y al resultado de la operación, potencia. En el caso de los números complejos calcular la potencia es algo intrigante, pero real. Por ejemplo, i elevado a la potencia i es aproximadamente igual a 0.20787957635 (recordar que i es la raíz cuadrada de -1).
La Función Zeta de Riemann es la expresión matemática que tiene la siguiente forma:
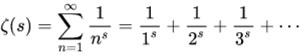
y la razón de su nombre es que para indicarla se hace una de la letra griega ζ, la cual se llama “zeta” (en inglés, ya que en español se le puede dar otros nombres). La variable s representa a un número complejo que es el exponente de cada una de los denominadores de las fracciones que se suman. Esta es la expresión matemática que aprendí un día en clase, y que a primera vista ya puede resultar misteriosa y compleja.
Raíces de las funciones
Si se considera la expresión f(x)=x2+1, uno puede reemplazar la variable x por el número especial i, resultando en la expresión f(i)= i2-1=0. Recordando que i2=-1 y (-1) +(1) = 0, entonces se dice que i es una raíz de f(x). Como las raíces son números especiales que pueden describir de una mejor manera a una función, resulta interesante saber cuáles son. Entonces, preguntar por las raíces de la Función Zeta de Riemann es una pregunta pertinente, pero sobre todo muy importante. Aprendí en mi clase de Variable Compleja que algunas de las raíces de esta función son los números de la forma -2n, donde n puede valen 1, 2, 3, etc. A estos se les conoce como “raíces triviales”. Pero, un análisis cuidadoso indica que puedan existir raíces con la forma 1/2 + ib, las cuales se conocen como raíces no-triviales.
Riemann quería determinar si todas las raíces no-triviales de la Función Zeta son solamente de la forma 1/2 + ib, y esto es lo que se conoce como la Conjetura de Riemann (Figura 2). Así es, está es la famosa conjetura que ha interesado e integrado a muchos matemáticos durante bastante tiempo.
Mediante el uso de las computadoras se han podido verificar que existen raíces de la forma en cuestión (raíces no-triviales), pero a pesar de que se han calculado millones de estos números no se ha podido afirmar mediante un argumento lógico que efectivamente todas las raíces de la Función Zeta de Riemann se encuentran sobre la línea vertical que pasa por el punto 1/2.
¿Por qué es tan interesante la Conjetura de Riemann?
Una de las razones (desde un punto de vista matemático) que hace interesante a un problema, es entender qué tantas otras cosas se obtienen al poder dar una solución a una determinada pregunta.
Saber que un número es la raíz de una función cobra mucha importancia cuando la raíz nos habla de las propiedades de la función que no se miraban claramente. Hoy en día se tienen computadoras que pueden calcular varias raíces (millones) de la Función Zeta de Riemann cuya parte real es 1/2. Aunque esto sólo muestra que existen algunas raíces con la forma conjeturada, lamentablemente no representa un argumento matemático para saber si “todos” los ceros no-triviales son efectivamente de tal forma.
Por lo que inmediatamente surge la duda, ¿por qué tratar de entender si la Conjetura de Riemann es verdadera o falsa, tiene alguna relevancia? Para vislumbrar un poco por qué ha sido interesante investigar la validez de la Conjetura de Riemann hay que recordar qué son los números primos.
Los números primos son números naturales que tienen la peculiaridad de que sólo tienen al uno y ellos mismos como los únicos divisores enteros. Por ejemplo, 12 puede dividirse de manera exacta por 1, 2, 3, 4, 6 y 12, que significa que no es un número primo, pero el número 19 si lo es (puedes hacer el ejercicio de comprobarlo). El conocimiento de los números primos se remonta a algo como dos mil años de la civilización humana. Ya Euclides los conocía (Euclides, “el padre de la geometría”).
Hay que recordar que los primeros números que las personas conocen son los números naturales como 1, 2, 3, etc. Se podría pensar que tales números son los números fundamentales de las Matemáticas, con ellos se pueden “construir” los demás tipos de números que se usan. Es aquí donde los números primos salen a mostrar su importancia. El resultado matemático conocido como el Teorema Fundamental de la Aritmética indica que cualquier otro número natural se puede representar como el producto de números primos. Por ejemplo, 15 es 3 por 5, y donde no es difícil verificar que 3 y 5 son números primos. Los números primos pueden considerarse de hecho como los números fundamentales o números atómicos (con la propiedad de que son indivisibles) y varios matemáticos así los consideran. Pero, aunque este resultado posee una belleza matemática, que para apreciarse con mayor amplitud es necesario tomar iniciativa, tomar un libro y comenzar a pensar sobre está rara belleza, ¿puede poseer alguna cualidad práctica o útil? Por ejemplo, cuando se crearon las primeras máquinas electrónicas de cálculo, entre las primeras cosas en las que se les utilizó, fue para hacer simulaciones. Esto se refiere a que una máquina genere aleatoriedad (azar), como se hace con el lanzamiento de un dado (no siempre se obtiene el mejor número para ganar un juego). Muchos otros algoritmos utilizados para investigar el comportamiento de los gustos de las personas o ver como se propaga una enfermedad, se deben inicializar de forma aleatoria. En muchos otros algoritmos como los usados en seguridad informática, también se necesitan generar la aleatoriedad y los números primos sirven para que estos cálculos sean eficientes y, claro ésta, confiables. Sin embargo, simular aleatoriedad y reconocer qué números son primos, son tareas nada sencillas.
La relación con los números primos y la Conjetura de Riemann se expuso tiempo antes de que el comenzará a estudiar a la Función Zeta. Euler, otro de los antiguos famosos matemáticos, estableció una relación entra la Función Zeta y los números primos que se encuentra expresada en la siguiente línea:
![]()
Es decir, la suma infinita, con la que se representa la Función Zeta, se puede ver como un producto infinito donde el índice (número que indica cuál son los factores de la multiplicación) considerado es un número primo.
Se puede establecer que, en caso de dar una respuesta clara a la Conjetura de Riemann, entonces se puede saber la ubicación de los números primos. Es decir, una vez que se conoce uno, se pueden saber dónde están todos los demás. Pero la conjetura tiene más implicaciones, su impacto en lo que se conoce como teoría de los números y geometría algebraica sería profundo. Además, la Conjetura de Riemann puede generalizarse, es decir, puede presentarse en un contexto más amplio, en el que se pueden abordar otras situaciones que son igualmente intrigantes y reveladoras.
¿Cuál ha sido la última noticia sobre la conjetura?
Recientemente, el 24 de septiembre de 2018, Michael Atiyah, famoso matemático británico de 89 años, en el Heidelberg Laureate Forum, realizado en Alemania, dio una conferencia donde anunciaba que había encontrado una prueba para la Conjetura de Riemann. El anuncio provocó muchas expectativas, considerando que Michael Atiyah es un renombrado matemático.
Después de la conferencia de Atiyah, muchas personas del medio matemático se quedaron con escepticismo sobre los argumentos dados. No están convencidos que estén ante argumentos sólidos y verificables. De los más o menos 20 renglones (aunque el documento donde se presenta la prueba es más extenso) sólo en una pequeña parte se encuentra lo esencial de la prueba de Atiyah para demostrar la conjetura. Esto parece ser un tanto misteriosos, ya que no dejan ver con claridad el por qué su demostración es correcta. Las funciones de Todd que Atiyah utiliza en su prueba, son objetos matemáticos poco conocidos (algunos incluso dicen que no se sabía de su existencia hasta Atiyah las menciono, son algo que sigue detrás de una cortina que no se ha desvelado). Otros piensan que las ideas expuestas por Atiyah son un tanto circulares, es decir, que usa lo que se quiere mostrar para mostrar que es cierto. Por ejemplo, de argumento circular es que, si quiero verificar que yo soy yo, entonces se puede decir que como yo soy yo, entonces soy yo, pero ¿esto es una manera real de comprobar que soy yo?
Es relevante mencionar que durante el tiempo que se ha tratado de probar que la conjetura de Riemann, también se ha intentado mostrar que es falsa. Se ha escrito mucho sobre las razones que llevan a pensar de qué falsa, pero, como puede suponerse, al momento nadie ha encontrado un argumento que verifique esto.
Ahora sólo queda esperar que se someta a un riguroso análisis las ideas de Atiyah, con la expectativa de quién revise el trabajo, lo cual puede llevar mucho tiempo (años), no comenta omisiones y así saber si se ha resuelto otro famoso problema matemático o se trata una falsa alarma.
Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos. Desde la Academia de Ciencias de Morelos externamos nuestra preocupación por el vacío que genera la extinción de la Secretaría de Innovación, Ciencia y Tecnología dentro del ecosistema de innovación estatal que se debilita sin la participación del Gobierno del Estado.
REFERENCIAS
1 https://francis.naukas.com/2 008/06/06/para-que-sirve-la- demostracion-de-la- conjetura-de-poincare-o- aplicaciones-del-flujo-de- ricci-al-cancer/
2 https://www.muyinteresante.es/ciencia/articulo/14-de-marzo-el-dia-del-numero-pi
3 https://riull.ull.es/xmlui/bitstream/handle/915/5797/Sustentacion%20aerodinamica%20y%20analisis%20complejo.pdf?sequence=1&isAllowed=y
Fuente: Academia de Ciencias de Morelos

