Grandes túneles cuánticos: el Premio Nobel de Física 2025

Carlos A. González Gutiérrez y W. Luis Mochán

Los Dres. Carlos A. González Gutiérrez y W. Luis Mochán son investigadores en el Instituto de Ciencias Físicas (ICF) de la UNAM. El Dr. Mochán es integrante de la Academia de Ciencias de Morelos.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

El Premio Nobel de Física 2025 le será otorgado a John Clarke, Michel H. Devoret y John M. Martinis, por su descubrimiento del tunelamiento cuántico macroscópico y la cuantización de la energía en un circuito eléctrico [1]. En este artículo le contamos de qué se trata esta historia.

Energía

Coloque una canica cerca del borde de un plato hondo sopero, suéltela y observe. Notará que la canica baja acelerando hacia el fondo del plato para subir al borde opuesto disminuyendo su velocidad hasta detenerse del todo (Figura 1). Después iniciará un movimiento similar de regreso. Esto se repetirá varias veces, pero llegando cada vez a una altura menor hasta quedar finalmente descansando en el fondo del plato, del que no escapará.

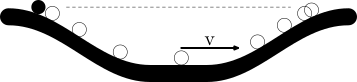
Esta simple experiencia ilustra una ley fundamental, la conservación de la energía. Al inicio la canica tiene energía potencial gravitacional, parte de la cual se convierte en energía cinética, energía de movimiento; la canica se mueve más rápidamente mientras más baja. Luego, al ascender, convierte su energía cinética en energía potencial, moviéndose cada vez con mayor lentitud hasta finalmente detenerse al regresar a la altura inicial. Las cosas son un poco más complicadas, pues conforme la canica rueda, golpea al plato produciendo sonido y calentándose, por lo que parte de su energía se disipa en energía acústica y térmica, impidiendo que llegue exactamente a la altura original. De experimentos como éste y muchos otros similares se deduce que existen varias formas de energía, pero la energía total de un sistema se conserva.

Para simplificarnos la vida concentrémonos en la energía potencial, que depende de la configuración (posición, orientación, etc.), y la energía cinética, que depende del movimiento. La energía potencial puede ser gravitacional, como en el ejemplo previo, o puede ser elástica (cuando se almacene en un resorte comprimido o en una liga estirada), podría ser eléctrica (cuando juntemos cargas que se repelan), o puede tener cualquier otro origen, pero se describe por una función U(x) que depende de alguna manera de la configuración x del sistema, como podría ser la posición. Podríamos describir la energía potencial del sistema mediante una gráfica (Figura 2).

Recordemos que la energía cinética de una partícula es proporcional al cuadrado de su velocidad, y que el cuadrado de un número es una cantidad positiva (más por más es más y menos por menos también da más). Por lo tanto, la energía cinética es positiva y la energía potencial es menor a la energía total; el sistema ¡tiene prohibido incursionar en regiones en las que su energía potencial supere a su energía total (Figura 3)! Así, una partícula con la energía E ilustrada en la fig. 2 sólo podría hallarse en el valle de la energía potencial del lado izquierdo, entre los puntos de retorno a y b, o en cualquier punto a la derecha del punto c, pero la cima entre b y c estaría vedada, así como la región a la izquierda de a (líneas horizontales punteadas).

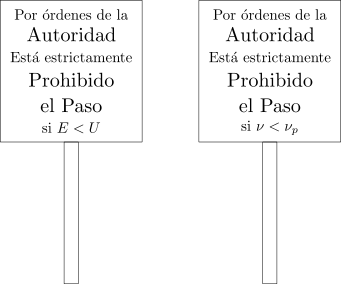
Ondas

Tome ahora una pieza de metal como una cuchara e intente ver a través de ella. Notará que es imposible. La luz no puede penetrar en el metal; los metales son opacos. ¿Por qué? La luz visible es una onda electromagnética, un campo eléctrico y un campo magnético que oscilan con una frecuencia que va de 400 a 790 terahertz (THz) (1 THz significa un millón de millones de oscilaciones cada segundo). Los metales tienen electrones que son acelerados por el campo electromagnético hasta que inducen un campo igual en magnitud pero opuesto al campo externo, apantallándolo, conduciendo a un campo total nulo, eliminando así la luz de su interior. Pero hay de luces a luces. Un metal se vuelve transparente si lo iluminamos con luz cuya frecuencia ν sea mayor a la llamada frecuencia del plasma νₚ del metal. Esto se debe a que si las oscilaciones se repiten en tiempos demasiado cortos, los electrones no alcanzan a moverse lo suficiente para apantallar al campo antes de que éste cambie de valor; el apantallamiento se queda rezagado. La frecuencia de plasma típica es mayor a los mil THz, que corresponde a luz ultravioleta, invisible a nuestros ojos. Por esto percibimos a los metales como opacos; toda la luz visible que llega a su superficie se refleja (Figura 3). Aprovechamos esto para fabricar espejos con vidrios lisos metalizando una de sus superficies.

Ondas evanescentes

Consiga una bolsa plástica metalizada como las que se usan para papas fritas o para envolver regalos. Colóquela, vacía y limpia, sobre una mesa, e ilumínela por el lado plateado. Verá que refleja la luz como si fuera un espejo. La capa metálica impide el paso de la luz, provocando su reflexión. Ahora espere a la obscuridad de la noche, cubra sus ojos con la bolsa y voltee la vista hacia algún foco encendido. Notará que un poco de su luz atraviesa la delgada película metálica y llega a sus ojos. En verdad, la luz sí puede penetrar en un metal, pero sólo una distancia muy pequeña, menos que una milésima de milímetro. Si la película metálica fuera más delgada que esta distancia, un poco de luz podría atravesarla. En el interior del metal sí puede haber luz, pero no en forma de una onda ordinaria, sino de una onda evanescente, esto es, que decae en una distancia corta (Figura 4).

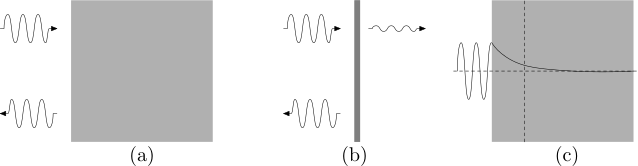
Partículas cuánticas

Hemos visto anteriormente que hay regiones que ni una partícula clásica (como una canica) ni una onda (como la luz) pueden penetrar. Sin embargo, vimos que las ondas sí pueden atravesar regiones prohibidas cuando éstas son suficientemente delgadas. El motivo es que las ondas en verdad sí penetran en estas regiones, pero lo hacen como ondas evanescentes que decaen en una distancia pequeñita. De acuerdo a la mecánica cuántica, esa teoría que revolucionó nuestra comprensión de la naturaleza en pequeñas escalas y cuyo centenario celebramos este año [2], las ondas se comportan como partículas y las partículas se comportan como ondas. Así, un electrón se comporta como una onda con una longitud de onda pequeñita, típicamente del tamaño de un átomo y miles de veces menores a la de la luz. Una consecuencia del comportamiento ondulatorio de un electrón es que puede escapar de barreras, atravesando regiones clásicamente prohibidas, como la cumbre entre b y c en la fig. 2, cuando la distancia entre b y c sea muy chica.

Tunelamiento

El fenómeno anterior se llama tunelamiento; las partículas cuánticas pueden atravesar barreras como si fueran montañas en cuyo interior se abriera un túnel (línea gris indicada por la letra t en la fig. 2), sin tener que ascender hasta la cima. El tunelamiento de electrones ocurre en distancias tan pequeñas como el tamaño de los átomos, pero explica muchos aspectos de la naturaleza química de la materia. Por ejemplo, explica cómo los electrones pueden escapar de ciertos átomos y ser atrapados por otros en el proceso de formar enlaces químicos. Además, el tunelamiento ha permitido desarrollar microscopios como el de tunelamiento de barrido (scanning tunneling microscope, STM, Figura 5) que han permitido ver átomos individuales en la superficie de sólidos y ver la función de onda de sus electrones [3]. Con el microscopio de tunelamiento incluso se han podido hacer animaciones de dibujos hechos con átomos individuales [4]. Algunos núcleos atómicos pesados pierden partículas debido al tunelamiento, fisionándose en fragmentos, lo cual explica la radiactividad.

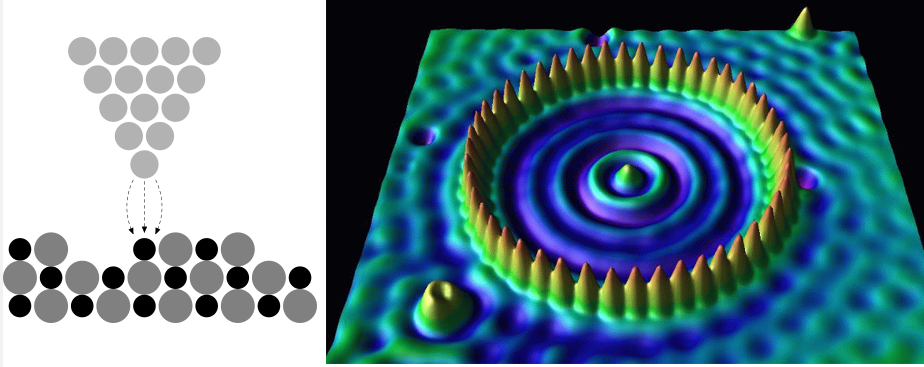
Hasta ahora hemos descrito como una partícula cuántica como el electrón puede atravesar regiones prohibidas cuando se encuentra atrapada en una barrera de potencial. Pero ¿sería posible que dos o más electrones pudiesen atravesar dicha barrera al mismo tiempo? Para convencer a las personas lectoras de que esto es posible, debemos primero discutir el fenómeno de la superconductividad.

Superconductividad

Los materiales como el cobre, oro, aluminio, etc., son buenos conductores de electricidad por tener electrones que pueden moverse libremente, con poca resistencia. A muy bajas temperaturas algunos materiales se convierten en superconductores, es decir, en materiales que pueden conducir electricidad sin resistencia o pérdida de energía alguna. Este fenómeno ha llamado mucho la atención por su potencial para múltiples aplicaciones tecnológicas como los trenes que flotan sin fricción, los aceleradores de partículas como el Gran Colisionador de Hadrones [5], detectores ultrasensibles de campo magnético, entre otras.

En este estado superconductor los electrones se unen en pares de Cooper, parejas de electrones que se mueven coordinados, como si fueran una sola partícula, como una pareja en un baile. Esto parece un poco raro ya que sabemos que dos partículas iguales, con la misma carga, tienden a repelerse. Sin embargo, en un superconductor esta repulsión se ve superada por una fuerza de atracción provocada por el movimiento de los iones positivos del material. Un electrón en movimiento atrae a los iones positivos cuando pasa cerca de ellos, deformando localmente al material y dejando tras de sí una estela de carga positiva concentrada, la cual puede atraer a otro electrón cercano, formando un par de Cooper [6]. A bajas temperaturas, millones de millones de pares de Cooper se condensan en un sólo estado cuántico imparable, como si formaran un ejército que marcha en una formación que no se puede romper, produciendo corrientes eléctricas que no disipan energía, no calientan al material, como una formación militar que no se desordena. Los pares de Cooper son partículas cuánticas que pueden atravesar barreras de potencial y dar lugar al tunelamiento.

La Unión de Josephson

Si dos materiales superconductores se separan por una barrera muy delgada de material aislante, los pares de Cooper pueden tunelear de un lado al otro sin disipar energía; la barrera no ofrece resistencia a los pares de Cooper, a pesar de corresponder a un material naturalmente aislante. Éste es el efecto Josephson [4]. A un dispositivo formado por un superconductor, un aislante y un superconductor se le conoce como unión o juntura de Josephson, en honor a Brian Josephson quien las describió en 1962. Si pasamos una corriente eléctrica a través de este dispositivo, el estado de todos los pares de Cooper se puede describir a través de una ecuación de movimiento parecida a la segunda ley de Newton para una sola partícula, fuerza es masa por aceleración, F=ma, justo como la canica de la que hablamos al inicio, con la diferencia de que el papel de la posición de la partícula corresponde a una variable que describe al estado colectivo de todos los pares de Cooper. La forma del potencial correspondiente resulta muy parecida al corte transversal de un lavadero para tallar manualmente la ropa, inclinado y con ondulaciones similares a las de la fig. 2. Queremos enfatizar que la partícula a la que nos referimos aquí y en adelante representa el estado macroscópico de millones de millones de pares de Cooper en el material superconductor. Controlando la corriente aplicada a la unión de Josephson podemos controlar la forma del potencial, pasando de un estado donde la partícula está atrapada entre dos puntos a un estado donde la partícula se puede mover a lo largo del potencial. En el estado donde la partícula está atrapada, como en el lado izquierdo de la fig. 2, no hay voltaje a través de la junta. En el estado donde sí se puede mover, como si disminuyéramos la altura de la primera cumbre en la fig. 2 por abajo de la energía E, se produce un voltaje proporcional a la velocidad. Medir el voltaje permite detectar si la partícula está atrapada o está en movimiento [6].

Alrededor de 1980 el físico teórico y premio Nobel de Física Anthony Leggett se preguntó si esta partícula macroscópica clásica (formada por numerosísimas partículas cuánticas acopladas) podría manifestar algún comportamiento cuántico. Como hemos visto, si se comportara como partícula cuántica podría escapar de pozos de potencial atravesando barreras mediante el efecto túnel, como si pasara del punto b al c en la fig. 2, y así generar un voltaje medible en una junta Josephson. Sería necesario garantizar que la partícula no gane energía robándola a sus alrededores y saltando por arriba de la barrera de potencial.

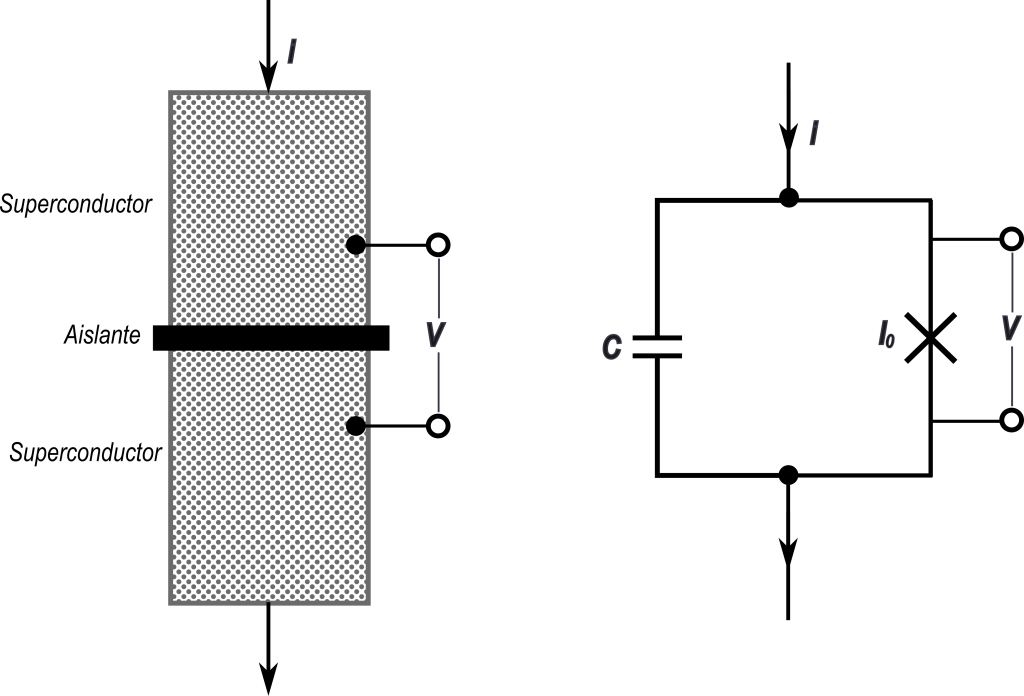
Para evitar esto, entre 1984 y 1985 los investigadores y ganadores del premio Nobel de Física de este año, J. Clark, M. Devoret y J. Martinis realizaron experimentos a muy bajas temperaturas usando un dispositivo como el mostrado en la fig. 6. En estos experimentos incrementaron poco a poco la corriente, registrando el valor para el cual aparecía un voltaje. Repitieron esto alrededor de cien mil veces a distintas temperaturas, obteniendo el umbral de la corriente eléctrica en el cual escapaba la partícula. El resultado fue que, al reducir la temperatura hasta un valor crítico, la corriente umbral comenzó a aumentar rápidamente debido al tunelamiento de la partícula macroscópica asociada al estado de los pares de Cooper que componen el dispositivo y que habría entrado al régimen cuántico. En este régimen cuántico macroscópico dicha partícula podría ocupar simultáneamente dos estados cuánticos distintos, dos configuraciones distintas de los pares de Cooper, como el famoso gato de Schrödinger que se halla en una superposición de vida y muerte a la vez. Los ganadores del premio Nobel también demostraron que la energía de la partícula macroscópica estaba cuantizada y no podía tomar más que ciertos valores, sin poder tomar valores intermedios. Esto confirma las predicciones de la teoría cuántica ¡pero aplicada ahora a sistemas macroscópicos!

El premio Nobel de física 2025 y la computación cuántica

La unión de Josephson que acabamos de describir no es más que un circuito eléctrico (Figura 6). Sin embargo, los experimentos de Clark, Devoret y Martinis demostraron que, bajo las condiciones adecuadas, dicho circuito puede comportarse como un átomo o una molécula real, mostrando efectos cuánticos como el tunelamiento y la cuantización de la energía. Estos resultados sentaron las bases para construir átomos artificiales con propiedades cuánticas basados en circuitos superconductores macroscópicos. Dichos átomos constituyen la unidad fundamental de información cuántica, el bit cuántico o qubit, que puede estar simultáneamente en una superposición de dos estados cuánticos que representen a los dígitos binarios 0 y 1, a diferencia de los bits clásicos que sólo pueden estar en el estado que representa al 0 o en el correspondiente al 1, pero nunca en una superposición de los dos. El uso de compuertas cuánticas superconductoras ha conducido a una de las arquitecturas más prometedoras para la implementación de la computación cuántica y actualmente lidera el desarrollo de procesadores cuánticos a gran escala [7].

Bibliografía

1. The Nobel Prize, Popular Information, https://www.nobelprize.org/prizes/physics/2025/popular-information/
2. Confinement of Electrons to Quantum Corrals on a Metal Surface, A. F. Crommie, C. P. Lutz, and D. M. Eigler, Science 262 (1993) 5131, 218-220 DOI:10.1126/science.262.5131.218.
3. IBM, A boy and his atom, https://www.youtube.com/watch?v=oSCX78-8-q0&list=PLaFe0BJiho2pbiULC7W4UpxFGArH7oD7i
4. R. P. Feynman, The Feynman Lectures on Physics, Vol. III Cap. 21, https://www.feynmanlectures.caltech.edu/III_21.html
5. El Gran Colisionador de Hadrones: Historias del laboratorio más grande del mundo, Gerardo Herrera Corral, (Ediciones Proceso, México, 2013).
6. The Nobel Prize, Advanced Information, https://www.nobelprize.org/prizes/physics/2025/advanced-information/
7. Superconducting Circuits for Quantum Information: An Outlook, M. H. Devoret and R. J. Schoelkopf, Science 339 (2013) 6124, 1169-1174 DOI:10.1126/science.1231930

Fuente: acmor.org