Arturo Olivares-Pérez

El doctor Arturo Olivares-Pérez es investigador de la Coordinación de Óptica del Instituto Nacional de Astrofísica Óptica y Electrónica (INAOE). Correo de contacto: olivares@inaoep.mx

Este artículo es un esfuerzo por tratar de visualizar y entender la magnitud colosal de la unidad de medida de longitud año luz, con elementos tangibles a nuestros sentidos.

Todo el mundo conoce un papel bond 29 kg tamaño carta, comúnmente usado para propósitos de impresión en casa; las dimensiones estándar rondan los 21.59 por 27.94 centímetros, con un espesor del orden de cien micras en promedio.

El ejercicio que mostraré se divide en tres momentos.

La primera parte consiste en acomodar hoja por hoja, una sobre otra, para visualizar una pila de hojas, con el propósito de saber cuántas de las mismas hay en un kilómetro de altura.

La segunda estriba en determinar a cuántos kilómetros equivale un año luz, tomando una conversión, considerando el espesor de la hoja (cien micras), asociándola como unidad de longitud a un kilómetro, con el objetivo de saber cuántas hojas hay y cuántos kilómetros representan un año luz con esta escala no convencional.

La tercera sección consiste en almacenar la pila de hojas en un edificio, calculando las dimensiones que debe tener para lograr ese propósito. Como verán más adelante, a pesar del esfuerzo para hacerlo tangible, se nos escapará de las manos.

Primera parte

¿Cuántas hojas hay en una pila de un kilómetro?

Para ello, elaboramos la siguiente tabla:

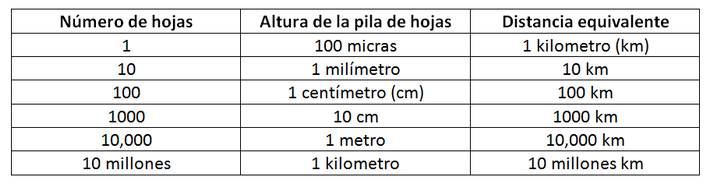
Segunda parte

¿Cuántos kilómetros tiene la unidad de medida año luz, de qué tamaño es la pila de papel en kilómetros que represente un año luz, y cuál es el número de hojas equivalente?

La velocidad de la luz es de 299,792.458 km/s; para propósitos divulgativos, esta cifra la redondearemos a 300,000 km/s.

Entonces, la operación para obtener los kilómetros sería convertir el año en segundos y después multiplicarlo por la velocidad de la luz para obtener la distancia en kilómetros, esto es:

(1 segundo) x (60 segundos) x (60 minutos) x (24 horas) x (365 días) x (300,000 velocidad de la luz).

Entendiendo que la unidad de medida adoptada como kilometro es el espesor de la hoja de papel bond, entonces, el número de hojas correspondería a los kilómetros representados como año luz. El número de hojas es de 9,460,800,000,000 = 9.4608 billones (millones de millones).

Ahora, hay que convertirlo en nuestra escala para visualizar ese número como una enorme pila de hojas de papel.

Para ello, dividimos pila de papel = 1 año luz (km)/10 millones km, teniendo: pila de papel = 946,080 km de altura. Sabiendo que la distancia promedio entre la Tierra y la Luna es del orden de 384,400 km, obtenemos que la pila de papel corresponde a 2.4611 veces la distancia promedio entre nuestro planeta y su satélite natural.

Tercera parte

Para almacenar todo ese papel, hay que calcular las dimensiones colosales del edificio.

Las aristas del papel bond tamaño carta son de 21.59 cm x 27.94 cm; entonces, el área del papel tamaño carta es de 603.2246 cm2; sabiendo que un metro cuadrado tiene 10,000 cm2, con esta información podemos conocer el número de hojas tamaño carta que caben en un metro cuadrado. Número de hojas = 10,000/603.2246 = 16.5775 hojas.

Con el cálculo de las áreas, al tener un edificio de aristas de 1km x 1km en el cual colocar 16.5775 millones de pilas de papel bond almacenadas, sería necesario uno con una altura de 57.07 metros; en otras palabras, un edificio de aproximadamente 20 pisos es del orden de 60 metros.

La reflexión en éste ejercicio es que, de alguna manera, se puede visualizar lo colosal de estas medidas, y expresarlas de esta manera nos ubica de forma más palpable a nuestros limitados sentidos en la realidad que nos rodea.

Fuente: elsoldemexico.com.mx