Rogelio Valdez Delgado

Obtuvo el grado de Doctorado en Matemáticas en Stony Brook University, Nueva York, en 2004 y realizó una estancia postdoctoral en el Instituto de Matemáticas de la Universidad Nacional Autónoma de México, unidad Cuernavaca. Desde el 2005 es Profesor Investigador de Tiempo Completo adscrito al Centro de Investigación en Ciencias de la Universidad Autónoma del Estado de Morelos (UAEMor) y es responsable desde 2010 del Cuerpo Académico “Álgebra, Geometría y Física Matemática Avanzados” del PRODEP. Pertenece al Sistema Nacional de Investigadores. Es miembro de la Academia de Ciencias de Morelos y actualmente es el presidente del Comité organizador de la Olimpiada Mexicana de Matemáticas a nivel nacional.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

Formas en la naturaleza

Tradicionalmente en la escuela nos enseñan conceptos propios de la geometría clásica o euclidiana, como el teorema de Pitágoras, o las fórmulas para calcular el área y el volumen de las distintas figuras geométricas que usamos en la vida diaria. Adicionalmente, se nos enseña otra geometría, que traduce estas figuras geométricas a expresiones algebraicas empleando funciones o ecuaciones; ésta es la geometría analítica. También nos enseñan el famoso número π que usamos para calcular el perímetro de una circunferencia, el área de un círculo, el volumen de una esfera y propiedades de muchas otras figuras. Estas geometrías se adaptan perfectamente a muchos aspectos de los objetos que los seres humanos hemos construido a lo largo de nuestra existencia.

Las herramientas matemáticas que aprendemos en el estudio de la geometría nos permiten estudiar y modificar el mundo en el que existimos, formado por cuerpos de formas relativamente simples como cuadrados, rectángulos, pirámides, círculos, etc.

Pero cuando observamos el mundo natural, es decir, aquello que no fue fabricado o modificado por los humanos, descubrimos que esas formas regulares no son comunes; nadie ha visto un lago cuadrado o una planta redonda. Entonces, nos preguntamos cómo podemos analizar las formas o la “geometría” de la naturaleza. Lograrlo nos permitiría analizar y descifrar los procesos naturales que ocurren a nuestro alrededor. Una respuesta a estas interrogantes es la geometría fractal que apareció a finales del siglo pasado.

La geometría fractal

La invención de la geometría fractal, hace apenas alrededor de 50 años, ha permitido explorar matemáticamente las complicaciones de muchas de las formas que aparecen en la naturaleza. ¿Cuál es la lógica que siguen las ramas de un árbol cuando crecen, los cauces de los ríos, los picos de las montañas, las trayectorias de los rayos en una tormenta, el ciclo de crecimiento de los microbios o la formación de las estrellas en una galaxia? Todos estos sistemas y muchos otros más se pueden tratar de entender y descifrar gracias a la geometría fractal.

“Las nubes no son esferas, las montañas no son conos, las costas no son círculos y la corteza de los árboles no es lisa, ni los rayos viajan en línea recta”, dijo Benoit Mandelbrot, el matemático que acuñó en 1975 el término fractal (del latín fractus, que significaquebrado o fracturado), quien tuvo la claridad para encontrar reglas y patrones en las formas aparentemente irregulares que encontramos en el mundo y traducirlas a un lenguaje matemático preciso.

Benoit Mandelbrot (1924-2010), nacido en Polonia, nacionalizado francés y luego estadounidense después de la II Guerra Mundial, tenía una mente extremadamente visual, lo que le permitió encontrar las bases matemáticas de los fractales, a pesar de que estas figuras parecían irregulares al ojo humano. En 1958 comenzó a trabajar para IBM en el Thomas Watson Research Institute de Nueva York, tras haber sido profesor en varias universidades americanas. Su objetivo era identificar por qué se producía “ruido blanco” en el sistema de telecomunicaciones en el que trabajaba. A grandes rasgos, se llama blanco a un ruido que contiene todas las frecuencias, todas ellas con la misma potencia, tal que ninguna sobresale sobre las demás, análogo a la luz blanca, la cual contiene una mezcla de todos los colores puros visibles.

Siguiendo su instinto de explicar los problemas en términos visuales, Mandelbrot estudió la gráfica que representaba la señal generada por el ruido blanco y descubrió que, independientemente de la escala de la gráfica, los datos de un día, una hora o un segundo, tenían siempre el mismo patrón. En 1967 publicó en la revista Scienceun artículo titulado “¿Cuánto mide la costa de Gran Bretaña?”, en donde expone sus ideas tempranas sobre los fractales. Fue entonces cuando recurrió a los trabajos de los matemáticos franceses Pierre Fatou (1878-1929) y Gaston Maurice Julia (1893 – 1978), quienes habían estudiado la iteración de ciertas funciones. Aquí, iteración significa evaluar una función f en un valor z de su dominio, f(z), luego evaluar la función nuevamente en este resultado, para obtener f(f(z)), esto es, iterar dos veces o hacer una iteración de orden 2, para luego evaluar la función nuevamente en el nuevo resultado y obtener f(f(f(z))) (iteración de orden 3) y así sucesivamente. Este proceso es la base de la propiedad de autosimilitud en matemáticas, la cual será abordada más adelante.

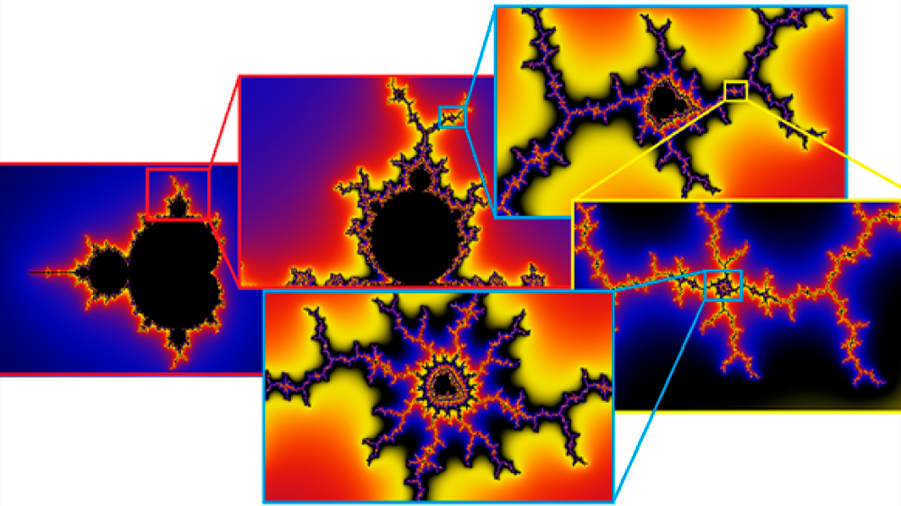
Gracias al potencial de las computadoras con las que trabajaba (que ahora nos parecerían obsoletas), Mandelbrot logró graficar la iteración de orden muy grande de una clase particular de funciones, los polinomios cuadráticos de la forma fc(z)=z²+c, donde z es la variable y c es un número complejo que juega el papel de parámetro constante, para obtener una de las imágenes más conocidas de la ciencia, el conjunto de Mandelbrot (ver figura 1). Cada punto en esta imagen corresponde a un valor de c, y el color corresponde al comportamiento de las iteradas del punto z=0 bajo la función fc. Esta curiosa imagen, con cierta semejanza a algo orgánico e irregular, es un ejemplo donde se presenta la propiedad matemática de autosimilitud que se tiene en los fractales, la cual puede ampliarse infinitamente, es decir, el patrón de los bordes o frontera se repite una y otra vez al profundizar en la imagen.

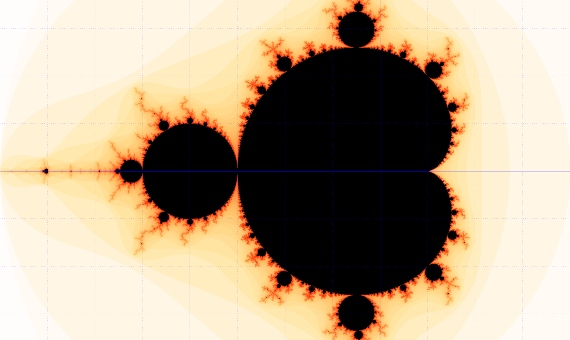
Mandelbrot fue el primero en tratar de modificar el hecho de que por siglos el mundo había sido explicado geométricamente a partir de formas idealizadas y volúmenes regulares con superficies lisas (líneas, círculos, conos, esferas), cuando la realidad es que nuestro mundo es áspero e irregular, pero también repetitivo y progresivo.

El fractal es una invención matemática

La palabra fractal está compuesta por dos partes, la primera parte proviene del latín fractus (quebrado ofracturado) y la segunda parte es el sufijo -al (que significa relativo a), como por ejemplo en la palabra mineral. La palabra fractus es un adjetivo, participio pasivo del verbo frangere (romper, quebrar, partir) de donde tenemos también las palabras fracasar, fracción y fracking.

En matemáticas, a grandes rasgos, un fractal es un objeto geométrico que, a partir de un patrón de repetición y a diferentes escalas, reproduce ciertas propiedades de sí mismo. Dicho de otra forma, un fractal es un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas. Pero seamos claros, los fractales como tal no existen en la naturaleza, el concepto anterior de fractal es una invención de las matemáticas. De hecho, debido a la complejidad del conjunto de Mandelbrot, la definición formal de fractal ha ido cambiando a lo largo de los años.

En la actualidad, en el mundo de las matemáticas, existen dos características esenciales que definen un fractal: primero debe ser un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas (autosimilitud); además su dimensión fractal es un número no entero, mayor que su dimensión topológica. Para la comprensión de los conceptos de dimensión y de autosimilitud se requiere un poco más de información que presentaremos a continuación.

La dimensión conocida contra la dimensión desconocida

Analicemos primero el concepto de dimensión. La palabra dimensión puede tener distintas definiciones en las diferentes áreas de las matemáticas. Para lo que nos concierne aquí, y como un ejemplo de dimensión, pensemos un momento en el concepto de dimensión espacial (euclidiana) de uso común, ya que nosotros existimos en un espacio de tres dimensiones en el que tenemos tres pares de direcciones: arriba-abajo, derecha-izquierda y delante-atrás; los objetos tienen largo, ancho y alto. Una figura como un cuadrado o un rectángulo tienen dos dimensiones, una línea representa una sola dimensión, y todo punto tiene dimensión cero. Como vivimos en un espacio de tres dimensiones, podemos ver objetos en tres dimensiones y en dimensiones más pequeñas. Por ejemplo, una hoja de papel suele representar un objeto de dos dimensiones (si ignoramos su pequeño grosor), al trazar con gis un segmento recto o curvo en un pizarrón, representamos un objeto de dimensión uno; además los puntos, que no podemos observar pero que podemos representar como pequeños discos de radios muy pequeños, tienen dimensión cero. Sin embargo, no podemos observar, identificar, reconocer a simple vista objetos de dimensión cuatro o mayor.

En 1884, el escritor inglés Edwin Abbott Abbott, que en un destello de originalidad y buen humor usó el seudónimo “A Square” (A al cuadrado), publicó la novela satírica Flatland (Planilandia) en la que nos habla de un mundo bidimensional. Es una obra especialmente popular entre estudiantes de matemáticas, física y ciencias de la computación, ya que su fácil lectura resulta útil para estudiar el concepto de múltiples dimensiones. Como obra literaria, Planilandia es un ejemplo de sátira sobre la jerarquía social imperante en la época victoriana. El narrador o personaje principal es un Cuadrado que nos lleva a conocer algunas implicaciones de vivir en dos dimensiones. En sueños visita un mundo unidimensional (Linealandia), donde intenta convencer al rey de ese mundo de la existencia de una segunda dimensión, lo cual resulta incomprensible para los habitantes de Linealandia. De la misma forma visita Puntilandia, la cual está compuesta por un solo punto que solamente tiene consciencia de su propia existencia ya que lo ocupa todo y no sabe de nada aparte de sí mismo. El Cuadrado recibe la visita de una esfera tridimensional, que le muestra el mundo en tres dimensiones. La mente del Cuadrado se abre a nuevas dimensiones paralelas, y trata de convencer a la esfera de la existencia de otras dimensiones diferentes a las conocidas por ella. Cuadrado lleva estas ideas a los habitantes de Planilandia, situación que lo lleva a terminar en prisión por sus intentos de corromper el pensamiento cerrado que había en Planilandia, donde todo estaba establecido en esas dos únicas dimensiones. Impotente, queda encerrado anhelando que alguien más se encuentre algún día con sus memorias.

Tal vez no podemos ver objetos de dimensiones mayores que tres, aunque matemáticamente sabemos que existen; pero más sorprendentemente existen objetos cuya dimensión (con otra definición distinta a la de dimensión euclidiana) es un número no entero. Para entender esto, regresemos a nuestro objetivo de definir la dimensión adecuada para un objeto fractal. Como siempre en matemáticas, sería ideal que esta nueva definición sea una generalización de alguna ya establecida para otros objetos matemáticos.

La dimensión fractal es una generalización de la dimensión euclidiana. De hecho, existen varias definiciones de dimensión que se aplican para fractales, aquí usaremos la llamada dimensión de homotecia. Consideremos un segmento (el cual tiene dimensión 1) de longitud 1, que se parte en segmentos, que son copias más pequeñas del segmento original, de longitud 1/L para obtener N(L)=L partes (ver figura 2), de esta manera cada una de las N(L) partes obtenidas mide 1/L, cualquiera que sea L, por lo que obtenemos de nuevo la unidad al multiplicar N(L) x (1/L) ¹ = L x (1/L) ¹ = 1, donde hay que notar el exponente 1 que acompaña a 1/L.

Ahora, si el objeto inicial es un cuadrado (el cual tiene dimensión 2) de área 1, cuyo lado se divide en segmentos de longitud 1/L (figura 2), el número de cuadraditos (que son copias más pequeñas del cuadrado original) de lado 1/L necesarios para recubrir todo el cuadrado de lado 1 es N(L)=L x L=L², por lo que tenemos N(L) cuadraditos, cada uno de área (1/L) ², por lo que el área total de todos los cuadraditos es nuevamente 1, es decir, N(L) x (1/L) ² = 1, donde ahora el exponente de 1/L es 2. Si, por último, tomamos un cubo (el cual tiene dimensión 3) de volumen 1, y lo dividimos en N(L)=L x L x L=L³ unidades más pequeñas (figura 2), es decir, en cubos (que son copias más pequeñas del cubo original) de arista 1/L, cualquiera que sea L, entonces tendremos N(L) cubitos, cada uno de volumen (1/L) ³, por lo cual se tiene que N(L) x (1/L) ³ = 1, y ahora el exponente es 3.

Este exponente es la clave para definir la dimensión que nos interesa, pues generalizando lo anterior, la dimensión fractal de un objeto geométrico es d si N(L) x (1/L) ͩ = 1, donde N(L) es el número de objetos (copias más pequeñas del objeto geométrico original) de tamaño 1/L, que recubren el objeto considerado. De donde deducimos, despejando d de la igualdad anterior, que d= log (N(L)) / log(L) es el número buscado, donde log es la función logaritmo. Notemos que, con esta definición de dimensión, un segmento sigue teniendo dimensión 1, un cuadrado sigue teniendo dimensión 2 y un cubo sigue teniendo dimensión 3.

Las partes son iguales al todo

La otra parte de la definición de un fractal es el concepto de auto similar. En matemáticas, la autosimilitud, a veces llamada auto semejanza, es la propiedad de un objeto en el que el todo es exacta o aproximadamente similar a una parte del objeto mismo; por ejemplo, en un helecho podemos comprobar que la forma de las hojas más grandes se repite en las hojas más pequeñas y también en sus bordes que se asemejan a pequeñas hojas. Aquí se manifiesta cierto tipo de autosimilitud, cada una de las partes de las hojas tienen la forma de un helecho completo. Otro ejemplo es el brócoli romanesco (ver figura 3).

El término autosimilitud se usa informalmente para diferentes conceptos matemáticos. Todas las formas o expresiones de autosimilitud implican un parecido estructural entre un objeto geométrico y una parte de este, es decir, existe parecido a diferentes escalas. Matemáticamente pueden distinguirse los siguientes tres tipos de autosimilitud: autosimilitud exacta o estricta, como la que aparece en objetos matemáticos, como el copo de nieve de Koch que veremos a continuación; autosimilitud aproximada como la que aparece en la naturaleza, un brócoli romanesco es un ejemplo muy ilustrativo de este tipo de autosimilitud; y la autosimilitud estadística, la cual es el tipo de autosimilitud más débil en que el objeto tenga medidas numéricas o estadísticas que se preserven con el cambio de escala, esto se da en muchos objetos del mundo real, como las costas marítimas, que son estadísticamente autosimilares, es decir partes de ella muestran las mismas propiedades estadísticas en diversas escalas.

El copo de nieve de Koch

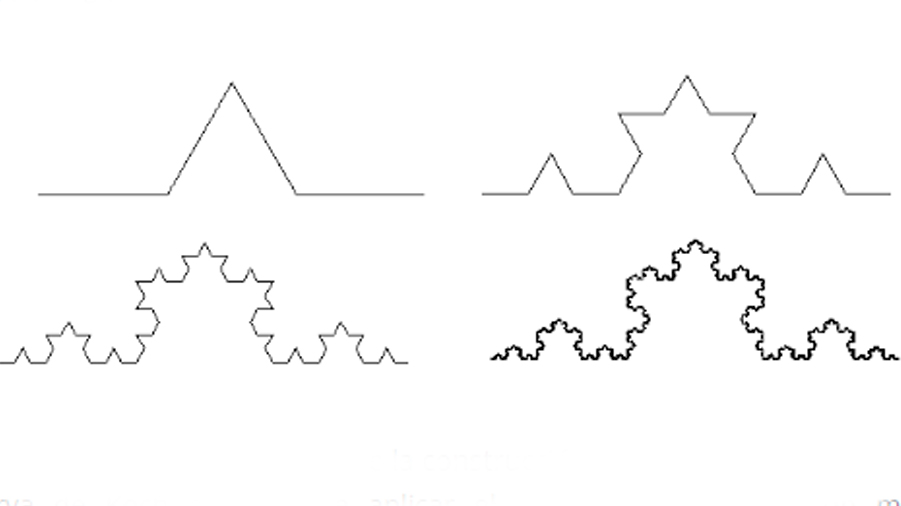
Un ejemplo básico de una curva fractal es la curva de Koch o copo de nieve de Koch, descrita por el matemático sueco Helge von Koch en 1904 en un artículo titulado “Acerca de una curva continua que no posee tangentes y obtenida por los métodos de la geometría elemental”. Para construir la curva se toma un segmento de cualquier longitud, se le divide en tres partes iguales, se remplaza la parte central por dos partes de igual longitud haciendo un ángulo de 60 grados, formando dos lados de un triángulo equilátero, para de esta manera obtener la curva del primer paso de la construcción (ver figura 4). Luego, con cada uno de los cuatro segmentos que forman la curva obtenida, se procede de la misma manera, lo que da lugar a 16 segmentos más pequeños en la segunda iteración, formando la curva del segundo paso de la construcción. Y así sucesivamente hasta el infinito (ver figura 4). En cada paso de la construcción de la curva de Koch, la longitud de la nueva curva es un tercio mayor que la anterior, es decir, la longitud de la curva aumenta en cada paso de forma constante; o lo que es lo mismo, cada curva tiene una longitud que es 4/3 la longitud de la anterior, por lo que la figura reducida un tercio cabe cuatro veces en la curva de tamaño original, es decir, N(L)=4 y 1/L=1/3, de donde se puede ver, con la fórmula descrita arriba, que su dimensión fractal es d = log (4) /log (3) = 1.2618, aproximadamente, un número no entero.

La fractalidad parcial de la naturaleza

El impacto de entender a los fractales es que la geometría fractal permite descubrir que algunos de los fenómenos naturales considerados irregulares o caóticos tienen, de hecho, un patrón y forma específica y una característica en común: son autosimilares. Esto quiere decir que su forma se repite en copias más pequeñas dentro de ella. El ejemplo más usado por Mandelbrot fue el ya mencionado brócoli romanesco, una verdura de apariencia arbórea que crece de tal manera que su forma y estructura están compuestas por pequeñas versiones geométricas de sí misma (ver figura 3). Cada parte es similar al todo, aunque estas sean más y más pequeñas. Algo similar se puede apreciar en el helecho común.

La matemática fractal ha sido muy bien recibida por los matemáticos, adoptada y aplicada en la actualidad, no solamente sirve para entender sucesos y formas naturales, se aplica en distintas disciplinas, incluyendo la genética, la astronomía, la medicina, la ingeniería, la música, las artes visuales y la animación.

Árboles, costas, helechos, montañas, copos de nieve, nubes y rayos, al observarlos sabemos que hay algo que tienen en común, una sensación intuitiva tal vez, pues entendemos que su complejidad se reproduce y se ramifica mientras cambia de escala. Se trata de la autosimilitud en la que pensó Mandelbrot. La geometría fractal permite encontrar un número que define y predice el comportamiento de este fenómeno; señala que el mundo es en su totalidad fracturable, y que al descomponer sus componentes aparecerán pequeñas porciones con explicaciones implícitas. La geometría fractal permite comprender y anticipar comportamientos que antes eran imposibles de explicar en la naturaleza, algo que puede ser tan inestable e irregular como la formación de las nubes, la estructura de los copos de nieve, la formación de montañas y ríos, el vuelo de las aves, entre otros, todos ellos fenómenos tan inmensos, como diminutos en sus partes.

Referencias

Abbott, A. A. Flatland: A Romance of Many Dimensions (By a Square). Bibliotech Press, 2018. ISBN 978-1618952851.

Addison, P. Fractals and chaos: an illustrated course. CRC Press, 1997. ISBN 978-0750304009.

Koch, H. von. Une méthode géométrique élémentaire pour l’étude de certaines questions de la théorie des courbes planes. Acta Math. 30, 145-174, 1906. (Reproduce y amplía el artículo de 1904, puede consultarse online en archive.org).

Mandelbrot, B. The Fractal Geometry of Nature. San Francisco: W.H. Freeman, 1983. ISBN 978-0-7167-1186-5.

Fuente: acmor.org