Dr. Adrián Ortega y Ing. Fernando Espitia

Adrián Ortegaes investigador postdoctoral en Física en el Wigner Research Centre for Physics en Budapest, Hungría. Su campo de investigación incluye transporte cuántico y recientemente cómputo e información cuántica.

Fernando Espitiaes Ingeniero Mecatrónico y recién egresado de la Licenciatura en Filosofía. Además,es seminarista en el Instituto de Estudios Eclesiásticos del Seminario de Guadalajara, México.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

Una nueva revolución cuántica

La segunda revolución cuántica está aquí [1]. Las computadoras cuánticas están disponibles en la nube, China ha logrado comunicación satelital segura basada en comunicación cuántica y la Unión Europea está por implementar el primer esquema de comunicación cuántica entre estados miembros. Hemos pasado de comprender sistemas cuánticos compuestos de muchas partículas al exquisito control de átomos individuales, y más adelante a la construcción de sistemas más complejos “pieza por pieza”. Sin embargo, esta construcción de tecnología de punta podría ocultar preguntas más elementales, por ejemplo, ¿esto implica que los científicos tienen una comprensión completa de los fenómenos cuánticos? ¿El avance tecnológico implica comprensión científica?

El siglo pasado, el físico húngaro-americano Eugene P. Wigner (Premio Nobel en Física 1963) propuso un interesante “experimento” que, entre otras cosas, involucra una discusión sobre los límites (en términos de conocimiento humano) de la interpretación tradicional de la teoría cuántica. Las comillas en la palabra “experimento” indican que es un experimento similar, en espíritu, al del gato de Schrödinger, que algunos lectores conocerán [2]. Nuestro objetivo es describir el “experimento” de Wigner y presentar a la audiencia preguntas que, hasta la fecha, quedan sin resolver con respecto a los fenómenos cuánticos. Este “experimento” sin resolver tiene un tinte filosófico. De hecho, en este experimento no es claro decir donde termina la “física” y donde comienza la “filosofía”. En una época de constante enfoque en la ciencia y sus profundas especializaciones pensamos que es importante y valioso recordar esta conexión a las personas, la cual estudia precisamente la subdisciplina de Filosofía de la Física.

El sistema de dos niveles: ingrediente esencial

Los conceptos de sistema (de dos niveles) y medición son cruciales para entender el amigo de Wigner. En los fenómenos cuánticos estos dos conceptos pueden parecer un poco extraños al principio; acostumbrándose un poco a ellos se vuelven (esperamos) naturales.

Como el concepto de medición puede llegar a ser más intuitivo que el de “sistema”, consideramos primero este último. Un “sistema clásico” puede ser simplemente una caja llena de pelotas etiquetadas al azar H y V. En teoría cuántica, tal vez el sistema más simple y no trivial es conocido como “sistema de dos niveles”[1]. Este es un nombre muy general que describe fenómenos similares. De hecho, un colega nuestro, en este periódico (ver [3]), describió un ejemplo de un sistema de dos niveles: la luz posee una propiedad llamada polarización y se puede preparar experimentalmente luz con dos estados de polarización, horizontal y vertical. A los físicos les gusta simplificar las cosas, así que, en lugar de hablar de polarización horizontal y vertical decimos que la luz con polarización horizontal corresponde a “{H}” y la vertical a “{V}”. {H} y {V} se les llama estados del sistema; cualquier sistema de dos niveles pueden ser representados por estos dos estados.

Hasta este punto, tanto el sistema clásico como el cuántico parecen iguales, ya que ambos tienen dos estados con etiquetas H y V, respectivamente. Abajo veremos cómo se diferencian uno del otro.

[1] Entiéndase esto como en la frase “todos los mexicanos son aquellos que nacieron en México. Uno a uno somos “diferentes”, pero compartimos la propiedad de haber nacido en México.

El experimento del amigo de Wigner

Wigner propuso este experimento pensado que vino a ser conocido como “El amigo de Wigner” en 1962 [4]. Es un experimento muy divertido e interesante que, entre otras cosas, postula la pregunta sobre el rol de una consciencia en el proceso de medición de un sistema cuántico. Para una lectura fácil, es mejor separar su explicación en tres partes: (1) describimos, por propósitos de comparación y claridad, como sería el caso en el que el amigo realizara el experimento en un sistema clásico, (2) tratamos el caso del experimento del amigo con un sistema cuántico y (3) describimos qué pasa cuando Wigner le pregunta a su amigo acerca del resultado del experimento.

El experimento clásico del amigo

En este caso, el amigo tiene una caja cerrada llena con pelotas, la mitad etiquetadas con H y la otra mitad con V (sistema= caja + pelotas mitad H y mitad V), ver Fig. 1a. Si el amigo toma una pelota al azar, tendrá 50% de probabilidad de obtener cualquiera de las dos etiquetas H o V, Fig. 2.b. La medición en este caso es el proceso en el que el amigo ve la etiqueta en la pelota que se sacó al azar. Más aún, si el amigo ve la etiqueta, digamos V, él sabe que antes de sacarla de la caja tenía la etiqueta V.

El experimento cuántico del amigo

Los fenómenos cuánticos son extraños porque posibilitan estados que no se encuentran clásicamente. En relación con el experimento mostrado arriba, el sistema tiene clásicamente dos posibles estados que escribimos como {H} o {V}. En cambio, si tenemos un sistema cuántico, antes de la medición es posible que el sistema esté en estados “inter-medios”[1]. Lo que esto significaría en el experimento previo y -atención, que esto es solo una analogía con el caso clásico- es que la pelota que saca el amigo, y antes de ver la etiqueta, ¡tendría ambas etiquetas! Justo después de la medición, el amigo verá sólo una de las etiquetas, pero no tiene manera de asegurar cuál era la etiqueta antes de la medición. Más precisamente, dichos estados inter-medios son “propios” del fenómeno cuántico, accesibles hasta cierto punto vía el proceso de medición, los cuales, en general, no tienen un equivalente con el caso clásico (ni siquiera un equivalente con probabilidad clásica como en el caso de la sección anterior).

[1] Para especialistas: estados “inter-medios” entiéndase como todo los estados en la superficie de la esfera de Bloch con polos norte y sur |H> y |V> , respectivamente.

Expliquemos con detenimiento. El amigo tiene en su laboratorio un sistema de dos niveles (digamos luz polarizada con estado ({H} Y {V})[1]) que decide medir en algún momento, ver Fig. 2. El sistema cuántico es de tal naturaleza que 50% del tiempo el amigo medirá (“verá”) H y 50% del tiempo “verá” V[2]. Si ahora la luz polarizada más el amigo (junto con todo el equipo experimental) es un nuevo sistema más grande, entonces después de la medición el estado sería: {H, amigo ve H} o {V, amigo ve V} con 50% de probabilidad cada uno.

[1] Ver nota 2. En general ({H} Y {V}) representa la combinación lineal a|H> + b|V>, a,b complejos tal que |a|^2+|b|^2=1; la probabilidad de medir {H} es |a|^2 y de medir {V} es |b|^2. Similarmente, ({H} Ó {V}) representa que existe la probabilidad clásica p de medir {H} y 1-p de medir {V}, con p real.

[2] Estas probabilidades se pueden modificar. Por ejemplo, el amigo puede medir H con 25% de probabilidad y V con 75%. Esto depende de las características del sistema que el amigo analice.

Los estados {H, amigo ve H} o {V, amigo ve V} son perfectamente compatibles con el caso clásico. ¿Dónde queda el estado “inter-medio” que mencionamos? En este caso la luz antes de la medición está en el estado inter-medio {H} Y {V} (llamado por los físicos “superposición”). Cuando el amigo mide (ve) el sistema, el amigo obtiene únicamente {H} o {V} con probabilidad de 50% cada uno. El proceso de medición induce una especie de “reducción” de ({H} Y {V}) a ({H} O {V}), y este es el famoso “colapso de la función de onda”.

Experimento de Wigner: Wigner le pregunta a su amigo/a acerca del resultado de su experimento

Sabemos lo que hace el amigo, ahora discutiremos qué pasa cuando Wigner le pregunta a su amigo/a qué es lo que vio. Esta es la parte más intrincada, pero en pocas palabras muestra explícitamente uno de los problemas inherentes del proceso de medición y el colapso de los estados inter-medios.

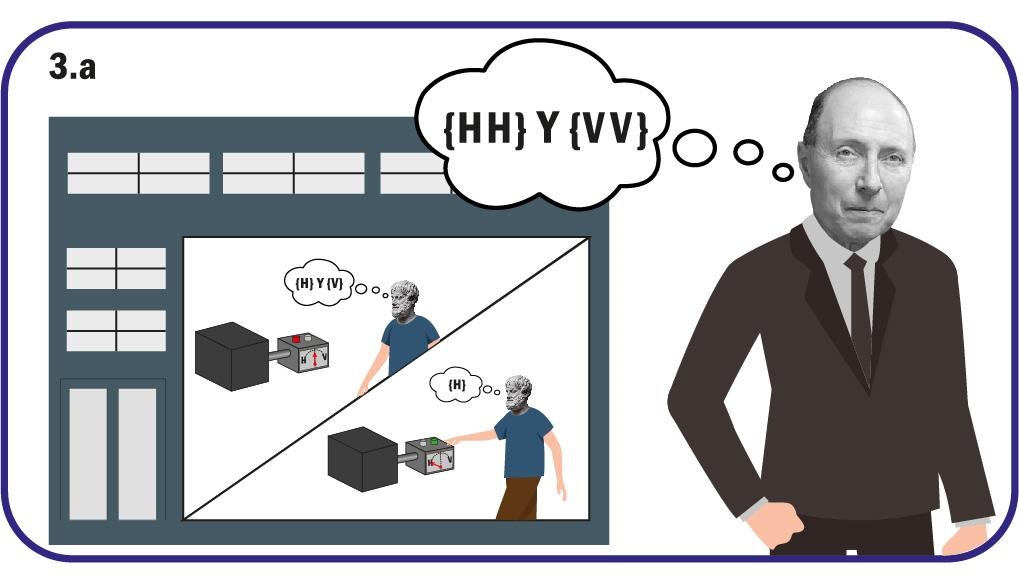
Veamos este caso con mayor profundidad. Wigner, que sabe algo de teoría cuántica, puede proponer cual es el estado de “todo el laboratorio”, esto es sistema de dos niveles + amigo antes de la medición. De acuerdo con las reglas de la teoría cuántica y el conocimiento sobre el experimento, para Wigner el estado combinado sistema + amigo es ({H} Y {V}) {amigo} antes de la medición del amigo, ver Fig. 3.a. Esto es, para Wigner su amigo posee el estado {amigo} que expresa el hecho de que el amigo no ha medido (visto) cual es el estado de la luz.

Justo antes de preguntar a su amigo, Wigner sabe que su amigo midió al sistema. Él concluye, usando las reglas de la mecánica cuántica expresadas en la interpretación de Copenhague (ver siguiente sección), que el sistema + amigo pasó por el cambio ({H} Y {V}) {amigo}→ {H, amigo ve H} Y {V, amigo ve V}. Si la respuesta del amigo fue H, entonces la “impresión” (de hecho, la medición) que Wigner obtiene es {H, amigo ve H}. Si la respuesta fue V, entonces la “impresión” de Wigner es {V, amigo ve V}, Fig. 3.b. Esto es lo que Wigner puede desarrollar y concluir usando el formalismo de Copenhague. Esta cadena de razonamientos que implica dicha interpretación, ¿son precisamente lo que corresponde a la experiencia empírica de Wigner al preguntarle a su amigo? ¿Podría ser que hemos saltado a la conclusión “demasiado rápido” y esta situación no es tal cual la hemos descrito? En la siguiente sección veremos precisamente donde nuestro razonamiento falla cuando lo comparamos con la experiencia empírica que tendría Wigner.

La paradoja y la importancia de la interpretación física

¿Dónde está entonces una posible discrepancia entre el razonamiento de Wigner y su experiencia empírica? El acertijo surge cuando uno se percata que Wigner no sabe cuándo el amigo hizo la medición. La única información que Wigner posee es que (1) el experimento fue realizado por su amigo y (2) el amigo midió antes de que Wigner le preguntara qué resultado obtuvo. Wigner no puede saber nada del colapso {H, amigo ve H} Y {V, amigo ve V} → {H, amigo ve H} O {V, amigo ve V} hasta que Wigner le pregunta a su amigo. En otras palabras, el cambio del estado que Wigner posee acerca del sistema + amigo fue alterado sólo cuando la información entró en la consciencia de Wigner.

La frase “entró en la consciencia” es aquí usada en un contexto muy específico y no debe generalizarse a otros contextos sin un cuidado considerable. El razonamiento es como sigue: Normalmente, los fenómenos cuánticos no pueden observarse directamente con “nuestros ojos”. Los átomos, moléculas y demás cosas cuánticas son “observadas” de una manera indirecta (quizá el sistema cuántico más accesible sea la luz, como los láseres). Encima de esto, uno tiene cosas “raras” como los estados inter-medios que vimos arriba. Nuestra intuición común no se lleva bien con los fenómenos cuánticos. La manera en la que los científicos pueden entenderlos y manipularlos es creando una teoría, en sus mentes, que se ajusta a los (complicados) experimentos que se pueden hacer sobre estos. La teoría de sistemas cuánticos es de alguna manera especial ya que se fundamenta fuertemente en lo que se llama interpretación. Muy crudamente, una interpretación es una “receta teórica” de cómo los sistemas cuánticos pueden entenderse (usando matemáticas). La típica, y que seguimos aquí, es la interpretación de Copenhague, pero de ninguna manera es la única que existe. Todas las interpretaciones de alguna manera padecen el mismo defecto: son una manera en la que nosotros como humanidad, inferimos cómo se comporta la naturaleza (cuántica). Coloquialmente hablando, es como si eligiéramos los lentes con los cuales vemos el mundo. Algunos lentes son buenos para ver cosas muy lejanas, otros para mirar de cerca. En este sentido no se han encontrado los lentes óptimos; sin embargo, la interpretación de Copenhague que aquí usamos es todavía aceptada entre los científicos y tiene una larga tradición de desarrollo y resultados.

La interpretación de Copenhague requiere a priori un sistema cuántico y un dispositivo de medición clásico, y no es nada claro dónde demarcar la frontera (movible) entre ellos (conocida como el “corte de Heisenberg”). Wigner da un paso más dotando al aparato de medición (amigo) con una “consciencia”. El rol de la “consciencia” aplica para Wigner o su amigo; antes decidimos resaltar solo el rol de Wigner porque es donde la paradoja aparece. Es precisamente aquí donde esta interpretación falla: Wigner tiene un rol como observador privilegiado, pero esto no tiene sentido. Si eso fuera verdad, sería equivalente a pensar que solo ciertos observadores tienen el “modo correcto” de ver los fenómenos, lo cual no tiene sentido porque la naturaleza está simplemente “ahí”: no tiene preferencia en revelarse a sí misma de una manera particular en condiciones equivalentes. Por ejemplo, podemos cambiar a Wigner ↔ amigo y ahora el amigo sería el observador privilegiado.

Por otro lado, para Wigner, hemos dicho que antes de que pregunte a su amigo, él considera el estado sistema + amigo como ({H, amigo ve H} Y {V, amigo ve V}) (equivalentemente ({HH} Y {VV})). Si el amigo hizo la medición, pero Wigner no ha hecho la pregunta, el estado ({HH} Y {VV}) en la mente de Wigner es incorrecto. La paradoja está justamente aquí: antes de la pregunta, pero después de la medición el amigo sabe que estado “ve” ({HH} O {VV}), pero para Wigner su “percepción” es todavía ({HH} Y {VV}). En palabras de Wigner: No es como si mi amigo estuviera en un estado de animación suspendida antes de contestar mi pregunta. Él ya ha decidido en su mente cuál es el resultado antes de la pregunta [4, nuestra traducción].

Un sistema cuántico también puede ser medido de manera indirecta acoplándose con otro sistema cuántico. Por practicidad, imaginemos que la polarización de la luz puede ser medida de esta manera usando un átomo. En este caso, la luz interactúa con el átomo y Wigner mide el átomo. Esta es una sustitución importante: el amigo (clásico) es reemplazado por un átomo (cuántico). Si hacemos esto, sorprendentemente la paradoja deja de existir. ¿Por qué ocurre esto? La razón es el rol del amigo, que posee algo como una “consciencia”, mientras que el átomo es suficientemente simple y, de alguna manera, mantiene la naturaleza cuántica sin alterar como la entendemos en la interpretación. Como Wigner dice: Se sigue que el ser con consciencia debe de tener un rol diferente en mecánica cuántica en comparación con el dispositivo inanimado de medición: el átomo considerado arriba [4, nuestra traducción].

Este experimento pensado ha podido ser reflexionado en la comunidad por muchas décadas. En la actualidad, el núcleo de la dificultad no es si “la entidad intermedia” (amigo o átomo) que “observa” el sistema posee una consciencia o no, más bien qué tan complicado (o complejo) tiene que ser para que nuestra interpretación falle. Su solución es todavía una cuestión abierta y debatida en la comunidad científica.

La filosofía como guía para la interpretación

El experimento del amigo de Wigner está íntimamente relacionado con el famoso problema de la medición. En el día a día, los físicos adoptan una actitud pragmática y trabajan principalmente con la interpretación de Copenhague. La solución del problema de medición es una tarea más filosófica junto con la búsqueda de una interpretación adecuada. En conexión con esto, una cuestión central en los fundamentos de la física cuántica es [5] si un estado cuántico es sólo una herramienta matemática para determinar probabilidades que existe solo en las mentes de los científicos, o si el sistema es “fielmente” representado por el estado cuántico abstracto (en términos técnicos esto es el dilema epistémico/ontológico).

En nuestra opinión, lo que es realmente interesante es por qué la física puede ser tan bien capturada por las matemáticas. El proceso es tan efectivo que podemos hacer, por ejemplo, predicciones físicas y diseñar tecnología, incluso si al final no se contestan todas las preguntas relevantes. Empezando por Galileo y Descartes, tendemos a pensar que la ciencia se encarga del problema de describir “la cosa real” entendida como “presente objetivamente” (esta distinción fue trabajada hasta cierto punto en [6]). No hay lugar para conceptos como “consciencia”. Quizá para tener una comprensión más clara de la ciencia, es necesario un cambio en la visión filosófica: una visión que no sea ni muy “mecanicista” ni muy “idealista”. ¿Qué tal un punto medio? Esto es de hecho posible, y un ejemplo es el movimiento fenomenológico iniciado por Edmund Husserl (matemático de formación), que podría brindar una visión renovada de la Mecánica Cuántica y la Física en general. La fenomenología de Husserl fue el origen de muchas aproximaciones filosóficas a las matemáticas y ciencias en general, y hay un interés actual en algunas ideas fenomenológicas desde la misma física. Aun así, la fenomenología es solo una propuesta entre muchas que estudian la relación entre las matemáticas y la realidad. Solo la continua investigación nos dirá qué tanto progreso puede hacerse cambiando el actual paradigma dominante.

Lecturas recomendadas

A. Clemente de la Torre. Física cuántica para filo-sofos. 1ra edición electrónica. Fondo de Cultura Económica (2010).
E. Husserl. La idea de la fenomenología. 1ra edición. Herder Editorial (2012).
Wigner, E.P., The unreasonable effectiveness of mathematics in the natural sciences. Richard courant lecture in mathematical sciences delivered at New York University, May 11, 1959. Comm. Pure Appl. Math., 13: 1-14 (1960).
Agradecimientos

Agradecemos a L. Bueno por amablemente proveer las figuras del artículo, a T. Kiss y M. Koniorczyk que revisaron la versión en inglés, y Y. Balderas y T. Clark por valiosos comentarios y sugerencias.

Referencias

1] Arturo Camacho. Aprendamos juntos. La segunda revolución cuántica: La llegada de la era cuántica. https://news.culturacolectiva.com/ciencia/que-fue-la-primera-revolucion-cuantica. Último acceso 2023-02.

[2] David Santaolalla. La paradoja del gato de Schrödinger RESUELTA. https://www.youtube.com/watch?v=lzxKZx7we4s. Último acceso 2023-02.

[3] W. Luis Mochán Backal. Entrelazados.

https://acmor.org/publicaciones/entrelazados. Último acceso 2023-02.

[4] E. P. Wigner. Remarks on the Mind-Body Question, pages 247–260, in Philosophical Reflections and Syntheses. 2nd printing. Springer, 1997.

[5] M. S. Leifer. Is the quantum state real? An extended review of ψ-ontology theorems. Quanta, 3:67, 2013.

[6] M. Heidegger. El ser y el tiempo. Fondo de Cultura Económica, 2009ed edition, 2009.

Fuente: acmor.org