El matemático británico de 89 años, Sir Michael Francis Atiyah, galardonado con los premios Abel y Fields, conocido por su contribución a la geometría y topología algebraica, anunció la prueba exitosa de la hipótesis de Riemann, una famosa conjetura que describe cómo los números simples se encuentran en una línea numérica.

El matemático de origen libanés presentará «una prueba simple usando un enfoque radicalmente nuevo» en la mañana del lunes, 24 de septiembre durante el Heildelberg Laureate Forum 2018. La comunidad matemática todavía permanece escéptica frente a la afirmación del matemático.

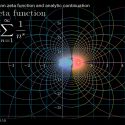
La hipótesis de Riemann es uno de los siete problemas del milenio, junto con la hipótesis de Poincaré y la teoría de Yang-Mills probada por Gregory Perelman. Está formulado de la siguiente manera. Tomamos una función: en cada punto s es igual a la suma de la serie:

Esta serie converge para S grandes. Con la ayuda de técnicas matemáticas especiales, es posible extender esta función a todo el plano complejo (donde obtenemos la función zeta de Riemann). Además, en algunos puntos del plano complejo, los valores de esta función resultan ser cero, por ejemplo, en puntos pares negativos.

Se dice que estos ceros reales son triviales. Pero aparte de ellos, hay otros ceros, complejos, por ejemplo, S = 0,5 ± 21,022040i. La hipótesis de Riemann afirma que todos los ceros no triviales de la función zeta se encuentran en la línea Re = 0.5 del plano complejo.

Riemann demostró que conociendo los ceros no triviales de la función zeta uno puede construir una función de distribución de números primos que muestra cuántos números primos no exceden un número dado. La validez de la hipótesis de Riemann permitirá probar las afirmaciones no relacionadas con los números primos, por ejemplo, en relación con la complejidad computacional de varios algoritmos.

La hipótesis de Riemann fue formulada en 1859 y aún no ha sido probada ni refutada. En el anuncio de su conferencia, Michael Atiyah señala que encontró una prueba simple, «basada en los trabajos de Neumann (1936), Hirzebruch (1954) y Dirac (1928)». De acuerdo con el programa de la conferencia, la duración de la conferencia será de solo 45 minutos.

Aunque Atiyah es un matemático galardonado con los premios matemáticos más grandes, muchos de sus colegas son cautelosos acerca de su declaración. Algunos comparan el intento de una simple prueba de la hipótesis de Riemann con la frase de Pierre Fermat de que «la evidencia ingeniosa era demasiado larga para llevarla al campo».

Michael Atiyah hizo una gran contribución a la topología algebraica, sentando las bases de la teoría K topológica. Uno de los resultados más famosos de las matemáticas es el teorema de Atiyah-Singer en el índice, utilizado en el análisis de ecuaciones diferenciales, por ejemplo, en física teórica.

Fuente: nmas1.org