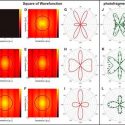
Un equipo internacional codirigido desde la Universidad Autónoma de Madrid (UAM) (España) ha obtenido la primera imagen directa del cuadrado de la función de onda de la molécula de hidrógeno. El experimento permite observar por primera vez la correlación entre dos electrones y explorar las implicaciones de esta interdependencia en las propiedades electrónicas.

Un equipo internacional de físicos y químicos ha desarrollado un nuevo método que permite observar directamente el cuadrado de la función de onda de los dos electrones que conforman el enlace de la molécula de hidrógeno (H2). El experimento permite identificar visualmente los distintos componentes que describen la correlación entre ambos electrones.

Aunque ya existen diversas técnicas que permiten deducir, en combinación con modelos sencillos, imágenes de las funciones de onda de electrones individuales en átomos y moléculas, este es el primer método que permite observar directamente la función de onda y, en concreto, la correlación entre dos electrones, así como explorar las implicaciones de esta dependencia mutua en las propiedades electrónicas.

Los resultados fueron presentados recientemente en Nature Communications por Investigadores alemanes, españoles, rusos y australianos, dirigidos por Reinhard Dörner del Goethe-Universität Frankfurt am Main (Alemania), y por Fernando Martín, investigador de la Universidad Autónoma de Madrid (UAM) asociado a los institutos IFIMAC e IMDEA-Nanociencia.

Según explica Martín, aunque hay otros métodos que permiten reconstruir correlaciones a partir de diferentes observaciones, esta es la primera vez que se obtiene una imagen directa de dicha correlación con solo mirar un espectro.

«Los espectros medidos son una imagen directa de las transformadas de Fourier de las diferentes partes del cuadrado de la función de onda. No se necesita reconstrucción, ni filtrado, ni transformación: el espectro refleja directamente las piezas de la función de onda en el espacio de momentos», detalla el investigador.

El nuevo método se basa en la detección simultánea del fotoelectrón y los fragmentos iónicos resultantes de la interacción de la molécula con la radiación sincrotrón. La combinación de ambas medidas permite determinar cómo se ve afectado el movimiento de un electrón (en concreto el fotoelectrón) por la interacción con el electrón que permanece en los fragmentos cargados. Así, el uso simultáneo de ambos métodos revela cómo se correlacionan los dos electrones y produce una imagen del cuadrado de la función de onda correlacionada de los dos electrones de la molécula H2.

Hay que hacer notar, sin embargo, que estas imágenes representan el cuadrado de la función de onda, y no la función de onda en sí misma.

“La función de onda no es observable en física cuántica, es decir, no se pueden obtener imágenes directas de ella –explica Fernando Martín–. Solo el cuadrado de la función de onda es observable, si se tienen las herramientas para hacerlo. Este es uno de los principios básicos de la física cuántica. Otros métodos utilizados para obtener la función de onda en sí misma en realidad lo que hacen es reconstruirla a partir de espectros medidos haciendo algunas aproximaciones. La función de onda nunca puede resultar de una observación directa.”

Los investigadores esperan que este nuevo enfoque se pueda usar también para obtener imágenes del cuadrado de la función de onda de moléculas con más de dos electrones, lo que implica detectar un mayor número de fragmentos de reacción. El método también podría permitir, en un futuro, visualizar correlaciones entre más de dos electrones.

Según Fernando Martín, el paso natural a seguir es probar un método similar en moléculas más complicadas. “Lo más probable es que el método funcione para moléculas pequeñas, pero no está claro si funcionará en moléculas muy complejas. No debido a limitaciones en la idea básica, sino principalmente debido a limitaciones experimentales, dado que los experimentos de coincidencia en moléculas complejas son mucho más difíciles de analizar debido a la existencia de un mayor número de grados de libertad.”

Fuente: noticiasdelaciencia