La exposición sobre textos encriptados en la época que va de los Reyes Católicos a Felipe II suscitó la polémica. Muchos argumentaron que, de ser tan deficiente o ingenuo el sistema criptográfico que se empleaba, España no habría sido dueña de un vasto imperio a nivel mundial. Sin embargo, la Historia y las Matemáticas (y las Ciencias en general) son totalmente compatibles, y tener conocimientos de ambas nos ayuda a entender mejor muchos aspectos del pasado y del presente.

Así, los métodos reflejados en los documentos históricos expuestos en el Archivo de Simancas se basan en la sustitución de letras, sílabas o palabras por símbolos u otras letras diferentes. Se los llama por ello cifrados de sustitución. El primero datado documentalmente en la Historia con propósitos políticos o militares se debe a Julio César y se puede leer en los volúmenes de “La guerra de las Galias”. Inicialmente lo que hizo fue algo tan sencillo como sustituir las letras romanas por letras griegas en sus mensajes. Pero no que se tradujera el texto al griego, sino algo mucho más simple: sustituir letras latinas por griegas. Y comenta que el enemigo fue incapaz de descifrar aquello porque pensaban que estaba en griego realmente.

Lógicamente, el ardid no pudo utilizarse mucho, ya que en todos los lugares y épocas hay alguien que acaba descubriendo el percal. Posteriormente, el propio César utilizó el procedimiento de trasladar cada letra de un mensaje tres lugares hacia adelante en el orden alfabético usual. En su honor se llamó a este procedimiento “cifrado César”, que no tiene por qué ser de tres lugares, sino que pueden ser cinco, siete, quince o el número de desplazamientos que se deseé. Para que quede claro el procedimiento, un ejemplo:

Mensaje: Hola, amigos.

Mensaje cifrado: KRODDPLJRV

Para complicarlo más, no ponemos los signos de puntuación (puntos, comas, etc.), y no separamos las palabras, sino que ponemos todo seguido, sin espacios.

Lo que se suele hacer para que la sustitución sea inmediata es colocar el abecedario normal en una línea (llamémosla alfabeto llano) y debajo otra línea con el alfabeto desplazado los lugares que hayamos decidido (tres en el caso de la cifra César). De este modo:

Se suele seguir la convención, en virtud de la claridad, de que el mensaje llano se escriba en minúsculas y el codificado en mayúsculas.

Limitaciones del sistema

Claramente, este método es bastante inseguro (débil, en el argot criptográfico). Solo hay 25 desplazamientos posibles de las letras (hay 26 letras, pero obviamente la posición en la que coinciden las letras del texto llano con las del codificado no sirve para nada; por tanto 25 posibilidades únicamente). Bastaría con tener escritas 25 tablas como la anterior, cada una con su desplazamiento (de dos, tres, cuatro, etc. lugares) y comprobar cuando vamos obteniendo algo coherente en las primeras letras. El descifrado es fácil y rápido. ¿Cómo se puede complicar? Por ejemplo, no desplazando las letras un número fijo de letras. Lo ideal: cualquier combinación de letras, lo que nos llevaría a 26! posibilidades (se lee 26 factorial; el factorial de un número es el producto de todos los valores enteros, en orden decreciente hasta el 1, o sea, 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720). Para 26! tenemos un número enorme: 403.291.461.126.605.635.584.000.000.

Así ya no es tan inmediato descifrarlo. Sin embargo, una disposición al azar de las letras hace necesario tanto al emisor como al receptor tener escrito en algún lugar la clave para poner en claro el mensaje. Y eso es un fallo de seguridad, porque el enemigo puede encontrar esa clave (que es, en parte, lo que les pasó a los nazis con los libros de claves para ajustar la posición diaria de la máquina “Enigma“; en el hundimiento de un submarino, los aliados recuperaron parte de los libros de claves, lo que permitió al sistema diseñado por Alan Turing no tener que ir una a una por todas las combinaciones, sino probar directamente las que aparecían en el libro. No fue tan simple, pero a grandes rasgos, eso sucedió). Esto es una regla de oro de la criptografía: el método no importa, lo que importa es tener bien segura la clave.

Complicando el sistema

Sin embargo, es muy fácil memorizar una palabra, y que ésta sea la clave para organizar las letras. Por ejemplo, acordemos como clave la palabra MATEMATICAS. Eliminamos de ella todas las letras repetidas: MATEICS, y coloquemos estas letras bajo las primeras del alfabeto llano. El resto las completamos según correspondan en el orden habitual. De este modo:

Así no tenemos que tener escrita nuestra clave en ninguna parte (es fácil recordar una palabra) con lo que no pueden descubrirla, y averiguar la palabra no es tan sencillo entre todas las del diccionario. Esta sustitución es bastante más segura que la de la cifra César. El mensaje “Hola, amigos” de antes quedaría como UDYMMZVSDJ. Aún más seguro sería utilizar como clave una palabra que no existiera, inventada.

Una amplia red de espías

¿Recuerdan las sustituciones que aparecían en los documentos utilizados por los Reyes Católicos, Carlos I y Felipe II? Todos se basaban en sustituciones en las que se necesitaba un papel en el que estaba escrita la clave. Y, desde luego, una de las cosas que deja muy clara la exposición del Archivo de Simancas es que en esa época había un gran entramado de espías en todas las ciudades europeas, y bastante hábiles. De modo que encontrar las claves para cifrar los mensajes no era demasiado complicado estando disponibles en alguna parte.

Pero es que el sistema de la palabra clave anterior, siendo más complicado, tampoco lo era mucho. Basta un análisis de frecuencia de las letras. Por tanto, la cifra de sustitución monoalfabética es vulnerable y descifrable fácilmente mediante análisis de frecuencia.

Lo que comentaba Simon Sighn sobre que al rey Felipe II le parecía brujería el que le entendieran todos los mensajes cifrados y su apelación al Papa -quien se moriría de la risa porque sus propios criptógrafos se encontraban entre los que los leían- es, aunque nos duela, absolutamente cierto y está documentado. La prueba es que no le hizo el mínimo caso. Sin embargo, a pesar de que los mensajes españoles fueran interceptados, no era recíproco y aquí no se conseguía descifrar nada. ¿A qué se debía?

El código indescifrable europeo

Se dice que hacia 1460, el arquitecto florentino Leon Battista Alberti, paseando por los jardines del Vaticano, se encontró con su amigo Leonardo Dato, el secretario pontificio, con quien se puso a debatir sobre criptografía. Este encuentro hizo que Alberti pensara en los métodos de sustitución monoalfabéticos, los únicos empleados entonces, y se le ocurriera utilizar no un alfabeto cifrado, sino dos a la vez, a fin de ponérselo más difícil a los criptoanalistas.

La idea era buena, pero desgraciadamente no se llegó a desarrollar hasta casi un siglo después. Aunque no está claro quién lo hizo con exactitud, lo cierto es que se atribuye al diplomático Blaise de Vigenère la conocida como “cifra Vigenère”, que utiliza 26 alfabetos distintos. Ahorrándonos pormenores históricos, lo primero que hacemos es componer un cuadro como el siguiente:

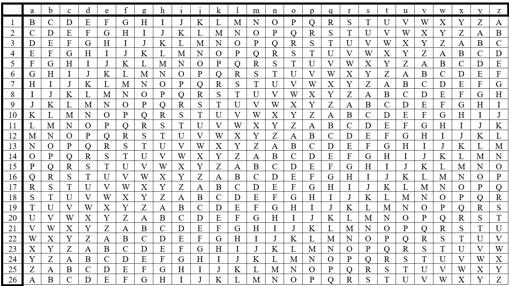
Con esta tabla podemos codificar nuestro mensaje con 26 alfabetos distintos. Obsérvese que la primera línea correspondería a un cifrado César con desplazamiento uno, la segunda con desplazamiento dos, etc. En la cifra Vigenère utilizaremos líneas diferentes del cuadro para cifrar las diferentes letras del mensaje. Dicho de otro modo, el emisor podría cifrar la primera letra según la línea 13, la segunda según la línea 9, la tercera según la línea 2, y así sucesivamente.

Como ejemplo cifremos el mensaje “Hola, amigos. Todo está dispuesto”, usando la palabra clave MATEICS (aunque ahora ya se pueden repetir las letras, pero dificulta más romper el código usar una clave inventada). Para empezar, repetimos la palabra clave tantas veces como necesitemos hasta completar nuestro mensaje. A continuación, buscamos la línea que empieza con la primera letra de la palabra clave, que es la M. Es la línea 12. Entonces miramos en esa línea donde va a parar la primera letra de nuestro mensaje, la h. Iría a la letra T. Y se va repitiendo el mismo proceso con cada letra. Quedaría algo así:

A una misma letra del mensaje pueden corresponderle letras diferentes en el texto cifrado. Como la codificación del mensaje depende de la palabra clave utilizada, un mensaje cualquiera puede codificarse de 26k modos diferentes, siendo k la longitud de la palabra clave. En el ejemplo anterior, como la longitud de MATEICS es 7, alguien que quisiera descifrar nuestra codificación con la fuerza bruta de un ordenador, por ejemplo, debería de probar con 26^7 posibilidades, lo que supone 8.031.810.176, algo más de unos ocho mil millones. Comparado con el número de combinaciones que se comentó en la sustitución monoalfabética de antes es mucho menor, pero la diferencia es que aquella era fácilmente rompible mediante análisis de frecuencia, y ésta no, además de que el número de claves a elegir es enorme. En su tiempo se le denominó la cifra indescifrable (“le chiffre indéchiffrable”).

De hecho, pasaron unos trescientos años hasta que Charles Babbage, uno de los padres de la informática, en el siglo XIX, logró descifrar un texto que le propusieron a modo de reto en 1854. No sería hasta 1863 cuando el oficial militar Friedrich Kasiski publicó por primera vez un ataque general a este método con éxito, si bien su trabajo no fue valorado en su justa medida hasta mucho después de su muerte. De hecho, otros autores como Lewis Carroll, publicaron artículos citando que la cifra Vigenère era inviolable, e incluso la revista “Scientific American” en 1917 así lo seguía manteniendo. Durante la Guerra Civil norteamericana, se utilizaron discos (el interno gira dentro del externo a la posición que se desee) que reproducen de un modo más cómodo el método descrito anteriormente en la tabla.

El método Kasiski para resolverlo

La principal debilidad de la cifra Vigenère es la repetición de la clave. Si un criptoanalista descubriera la longitud de esa clave, entonces el texto cifrado se trataría como varios cifrados César entrelazados que uno a uno podríamos romper con relativa sencillez. Esto fue descubierto por el oficial prusiano Friedrich Kasiski, quien lo publicó en 1863.

Por tanto, ponemos nuestra atención es las repeticiones. Las repeticiones de letras en el texto cifrado indicarían repeticiones en el mensaje original (no todas, pero sí algunas). La distancia entre esas repeticiones son una pista esencial para determinar la longitud de la clave. De hecho, los mensajes cifrados con este sistema producen muchas repeticiones. Consignamos todas ellas y la distancia entre las mismas, y gracias al máximo común divisor, se suele poder descubrir la longitud de la clave. Desde ahí todo es más sencillo. Lógicamente, cuanto más largo sea el mensaje interceptado, más información nos proporcionará, y más serán las herramientas con las que trabajar en la decriptación.

Podría pensarse que, gracias a la solidez del método, todos los países europeos utilizarían la cifra Vigenère. La realidad es que muchos pasaron de él. En el caso español tiene delito porque Gonzalo Fernández de Córdoba, el Gran Capitán, utilizaba métodos polialfabéticos en su correspondencia con el Rey Católico, no tan sofisticados como la cifra Vigenère, pero con la misma idea (unos 5 alfabetos diferentes en vez de los 26 descritos). ¿Por qué posteriormente Felipe II volvió a las cifras monoalfabéticas, absolutamente desfasadas en cuanto a seguridad? Trabajo para historiadores.

Consecuencias de un código débil

Lo que está claro es que hay algunos datos que, sin ser concluyentes, pueden darnos algunas pistas. Se sabe que el carácter del “rey prudente” era un tanto peculiar y “disfrutaba” de algunas obsesiones que quizá no le vinieron nada bien a la toma de ciertas decisiones. Como muestra, un botón: el día de Año Nuevo de 1567 promulgaba una Pragmática Sanción, edicto por el que se obligó a que los moriscos dejasen su modo de vida y costumbres en un plazo de tres años; en definitiva, por las razones que fueran, se les echó, como había ocurrido anteriormente con los judíos en la época de los Reyes Católicos. Esto trajo consigo el abandono de las ciencias, ya que un amplio sector de la población de ambos pueblos se dedicaba a estos menesteres (fueron los criptoanalistas árabes los que desarrollaron el análisis de frecuencia).

Consecuencias inmediatas: los barcos se hundían (encallaban por la desactualización de las cartas náuticas) y estábamos plagados de ingenieros italianos, flamencos y alemanes que, lógicamente, miraban más por los intereses de sus países que por los que les contrataban. En poco tiempo fue palpable el atraso en materia técnica en todos los órdenes, al que Juan de Herrera trató de poner arreglo, convenciendo al monarca de la pertinencia de formar a nuestros ciudadanos. Así, el 25 de diciembre de 1582 se estableció una Academia de Matemáticas y Arquitectura Militar en el antiguo Real Alcázar de Madrid. No obstante, las buenas intenciones quedaron en poca cosa.

Fuente: abc.es/ciencia