Antes de comenzar, quiero compartir un problema que, a lo mejor, muchos de los lectores recuerdan de sus primeros años en la escuela. El maestro contaba una historieta como esta:
Imagina que quieres embaldosar una habitación rectangular con baldosas cuadradas, todas del mismo tamaño, pero no te apetece romper ninguna baldosa. Digamos, por ejemplo, que las dimensiones de la habitación son 360 x 405 cm2. Además, te has empeñado en utilizar baldosas del mayor tamaño posible. ¿Cuáles deben ser las dimensiones de cada baldosa?
Ahora es cuando nuestro «profe» hablaba del máximo común divisor de dos números y explicaba que las baldosas cuadradas de lado igual a 45 cm eran las más grandes que permitían resolver el problema. Pura magia.
Es evidente que el problema no está del todo extraído del mundo real pero cumplía su objetivo de aclarar algunos conceptos aritméticos. Vamos a continuar por esa línea y plantear algunos problemas imaginarios del mundo de la albañilería matemática.
Así pues, imagina que has heredado una gran mansión y quieres alicatar una habitación de dimensiones infinitas, utilizando infinitas baldosas, todas iguales, y piensas que quedaría bonito si las baldosas tienen forma de polígono regular.
Después de algunos intentos, enseguida caes en la cuenta que sólo hay tres polígonos regulares que cumplen la normativa: triángulos, cuadrados y hexágonos. La prueba matemática es que son los únicos cuyos ángulos internos son divisores de 360 grados. La mejor aproximación de este problema al mundo real consiste en cubrir con losetas grandes extensiones, como alamedas, parques o avenidas. De hecho, no es difícil encontrar a nuestro alrededor calles pavimentadas con alguno de estos tipos de baldosas.
¡Qué curioso!, los polígonos regulares de tres, cuatro y seis lados permiten resolver el problema pero los pentágonos no sirven. Más aún, con cualquier tipo de triángulos y cuadriláteros, no necesariamente regulares, es posible también llenar el plano (juega tú mismo a teselar el plano con esta actividad del proyecto Descartes). Así que, de vuelta a tu mansión, te planteas el reto de embaldosar la habitación utilizando pentágonos, todos iguales aunque no sean regulares.
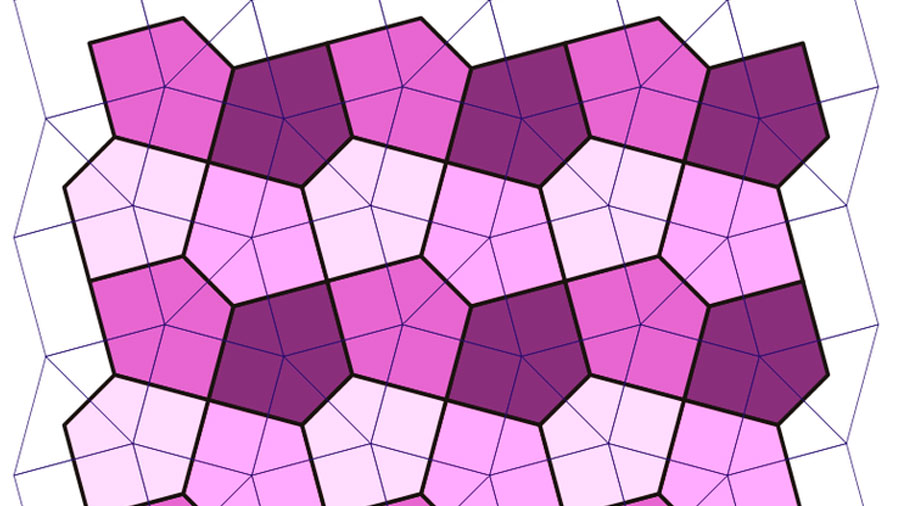
El problema no es tan sencillo como el anterior. Ahora bien, si has viajado por El Cairo y te has ido fijando en el suelo, habrás encontrado algunas calles pavimentadas con pentágonos, cuyos lados son todos iguales pero no así los ángulos.
Comprenderás que el colectivo matemático se interese por el tema y se plantee una cuestión más profunda: ¿cuántos tipos de pentágonos existen con los cuales se puede embaldosar una habitación infinita? En realidad, el problema interesa a los profesionales pero también atrae a los aficionados, sobre todo a los artistas, pues las posibles soluciones sirven de inspiración para sus creaciones.
Digamos que la historia comienza en 1918, cuando el matemático alemán Karl Reinhardt encontró cinco clases de pentágonos convexos que teselan el plano y aseguró que el proceso de encontrar otros tipos sería demasiado tedioso y probablemente no daría ningún resultado. En efecto, fue muy tedioso pero fructífero, pues, casi 50 años después, Richard Kershner encontró en 1967 otros tres tipos.
Cuando ya se creía que el problema estaba resuelto, en julio de 1975 Martin Gardner publicó un artículo recopilatorio titulado «Tiling with convex polygons» en la revista Scientific American, el cual tuvo mucha repercusión. Tanto que Richard James III, informático aficionado a las matemáticas, leyó la primera parte del artículo, pensó que se trataba de un acertijo y descubrió otro tipo de embaldosado pentagonal, el noveno de la lista.
Como se dice vulgarmente, la comunidad matemática desperdició una buena oportunidad de quedarse callada. Ya no podía haber ninguna seguridad de que el problema estuviera resuelto.
Ahora es cuando entra en escena Marjorie Rice, ama de casa nacida en 1923 en St. Petersburg (Florida) y madre de cinco hijos. A pesar de que su formación académica terminó en el bachillerato, el artículo de Gardner le inspiró a dedicar su tiempo libre en el problema. Con gran audacia, desarrolló su propio sistema de notación para representar las restricciones y las relaciones entre los lados y ángulos de los polígonos. Así, entre 1976 y 1977, logró descubrir cuatro nuevos tipos de teselaciones pentagonales. Una hazaña digna de admiración.
Posteriormente, la propia Marjorie Rice se dedicó a crear diseños artísticos basados en sus descubrimientos, como puede verse en el portal «Intriguing tessellations». El interés de los matemáticos por su trabajo se plasma en este documental de David Suzuki.
No termina aquí la historia, ya que el decimocuarto tipo de baldosa pentagonal fue descubierto por Rolf Stein en 1985 y hace un año se podía leer que desde entonces no se han encontrado más (todavía hay muchos lugares en internet que describen sólo los catorce tipos conocidos hasta ese momento, como este archivo de Geogebra).
En agosto de 2015, Alex Bellos anunció en The Guardian el descubrimiento de un nuevo tipo. Treinta años después del anterior descubrimiento, Casey Mann, Jennifer McLoud y David Von Derau, de la Universidad de Washington en Bothell, confiaron con éxito en que su ordenador pudiera realizar una búsqueda exhaustiva para dar a luz un nuevo caso (en la revista Tangente 167 puedes ver los 15 casos). ¿Será el último?
Observación final. Se ha demostrado que ningún polígono convexo con más de seis lados permite teselar el plano. El caso del hexágono fue tratado por Karl Reinhardt en su tesis doctoral de 1918, cuando probó que sólo hay tres familias de hexágonos convexos con los que se puede embaldosar un plano.
Es decir, el caso de los pentágonos es el único que no está completamente resuelto. ¿Te atreves a intentarlo? Te espera el Olimpo de las Matemáticas.
Fuente: abc.es